| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- CodeEngn
- Reflected
- 자료구조
- cgroup
- pwnable
- htmlinjection
- SISS
- 와이어샤크
- Systemhacking
- wireshark
- 유석종교수님
- acc
- fork-bomb
- basicrce3
- beebox
- Reversing
- backjoon
- datastructure
- Dreamhack
- System
- python
- c
- grafana
- mount
- EC2
- bWAPP
- AWS
- cloud
- Linux
- 백준
- Today
- Total
Ctrl + Shift + ESC
CHAPTER 04 스택과 큐 본문
4.1 스택
스택(stack) : 선형 리스트(linear list)의 특별한 형태, 책 또는 접시와 같은 물건을 한쪽 방향으로 쌓는 구조
후입선출(LIFO : Last-In, First-Out, 나중에 들어가는 원소가 가장 먼저 나옴) 구조이다.
스택 자료구조는 함수 호출 관리, 문법 검사, 수식 평가 등에 잘 부합된다.
스택은 다음과 같이 리스트로 표현할 수 있다.
a(0)는 스택 S에 처음으로 추가된 원소이고, a(n-1)은 가장 나중에 추가된 원소이다.
top은 마지막으로 추가된 원소를 가리키는 변수이다.

push : 스택에 원소를 추가하는 연산
pop : 스택에서 원소를 삭제하는 연산
리스트가 아닌 정적 배열에 스택을 구현하는 경우
push() 함수는 스택에 원소를 추가하기 전에 'stack full' 상태가 아닌지 검사한다.
pop() 함수는 스택에서 원소를 꺼내기 전에 'stack empty' 상태가 아닌지 검사한다.
top 변수가 -1이면 스택이 빈 상태임을 의미한다.
프로그램 4.1 스택의 구현
위 프로그램에서는 리스트를 사용하여 크기가 5인 스택을 생성한다.
파이썬 리스트는 크기 제한이 없지만 예제를 수행하기 위해서 size 변수로 스택의 크기를 지정한다.
원소(3, 4, 5, 6, 7, 8)를 순서대로 추가하면 마지막 원소(8)에서 'stack full'오류가 발생한다.
반대로 pop() 함수를 연속적으로 호출하면 6번째 호출에서 'stack empty' 메세지가 출력된다.
class Stack :
def __init__(self, size) :
self.top = -1
self.stack = []
self.size = size
def push(self, item) :
if self.top < (self.size-1) :
self.top += 1
self.stack.append(item)
self.fhow_stack()
else :
print("Stack full")
def pop(self) :
if self.top > -1 :
self.top -= 1
return self.stack.pop()
else :
print("Stack empty")
def show_stack(self) :
print(self.stack)
s = Stack(5)
for item in [3, 4, 5, 6, 7, 8] :
s.push(item)
for i in range(6) :
s.pop()
s.show_stack()코드를 살펴보았다.
class Stack :
def __init__(self, size) :
self.top = -1
self.stack = []
self.size = size처음 Stack을 만들 때 생기는 생성자이다.
Stack의 top을 -1로 저장해 스택이 비었음을 알린다.
stack에도 값을 넣지 않는다.
그리고 예제를 수행하기 위해 size를 입력받는다.
def push(self, item) :
if self.top < (self.size-1) :
self.top += 1
self.stack.append(item)
self.show_stack()
else :
print("Stack full")push() 함수를 통해 stack에 원소를 입력한다.
top이 size-1보다 작을 경우, (top의 시작은 -1이기 때문에 꽉 차면 size-1의 값을 가진다.) 즉 stack이 full이 아니면
top에 +1을 한 뒤에 stack에 입력받은 item을 추가한다.
그리고 show_stack() 함수를 통해 stack을 출력한다.
top이 size-1과 같은 경우 stack이 full이므로 Stack full을 출력한다.
def pop(self) :
if self.top > -1 :
self.top -= 1
return self.stack.pop()
else :
print("Stack empty")
def show_stack(self) :
print(self.stack)pop() 함수를 통해 stack의 원소를 삭제한다.
top이 -1이 아닐 경우, 즉 stack이 empty가 아닐 경우 top에 -1을 한 뒤에 pop() 함수를 통해 마지막 원소를 삭제한다.
top이 -1이라면 stack이 empty이므로 stack empty를 출력한다.
show_stack() 함수는 stack을 출력하는 함수이다.
s = Stack(5)
for item in [3, 4, 5, 6, 7, 8] :
s.push(item)
for i in range(6) :
s.pop()
s.show_stack()5칸짜리 Stack s를 만들었다.
s에 [3, 4, 5, 6, 7, 8]을 입력한다.
stack의 크기는 5이기 때문에 8을 입력할 때 stack full이 출력된다.
s.pop()을 통해서 마지막 원소를 삭제하고 결과를 출력한다.
5개의 원소를 삭제하고 6번째 반복문에는 더 이상 지울 원소가 없기 때문에 Stack empty가 출력된다.

아래는 스택의 상태를 표로 나타낸 것이다.
|
연산
|
[ 0 1 2 3 4 ]
|
top
|
결과/반환값
|
|
초기상태
|
|
-1
|
|
|
push(3)
|
3
|
0
|
|
|
push(4)
|
3 4
|
1
|
|
|
push(5)
|
3 4 5
|
2
|
|
|
push(6)
|
3 4 5 6
|
3
|
|
|
push(7)
|
3 4 5 6 7
|
4
|
|
|
push(8)
|
3 4 5 6 7
|
4
|
stack full
|
|
pop()
|
3 4 5 6
|
3
|
7
|
|
pop()
|
3 4 5
|
2
|
6
|
|
pop()
|
3 4
|
1
|
5
|
|
pop()
|
3
|
0
|
4
|
|
pop()
|
|
-1
|
3
|
|
pop()
|
-1
|
stack empty
|
4.2 선형 큐
큐(queue) : 작업들이 처리되기 전에 대기하고 있는 선형 리스트 자료 구조
선형 큐(linear queue) : 큐의 시작과 끝이 서로 분리되어 있는 구조
순환 큐(circular queue) : 양 끝이 연결된 구조
큐에서는 원소들이 선입 선출(First-In, First-out) 방식으로 도착 순서에 따라 추가되거나 삭제된다.
새로운 원소 a(n-1)는 큐(Q)의 가장 뒤(rear)에 추가되고, 큐의 맨 앞(front) 원소(a0)가 먼저 삭제된다.
front와 rear는 큐의 앞과 뒤 원소를 각각 가리키는 변수이다.

큐는 파이썬의 리스트를 이요하여 구현할 수 있다.
큐에 front와 rear 변수를 사용하여 큐의 앞과 뒤 원소를 가리키도록 한다.
push(또는 add) : 큐에 원소를 추가하는 연산, append() 함수 이용
pop(또는 delete) : 큐에서 원소를 삭제하는 연산, pop(0) 호출
→ 인덱스 없이 pop() 사용하면 리스트에 가장 나중에 들어간 원소가 삭제된다!
스택과 마찬가지로 원소를 추가하기 전에는 큐가 가득 찬 상태인지를 검사하고, 원소를 삭제하기 전에는 비어 있는 상태인지 확인해야 한다.
큐가 동적 배열인 경우 size를 통해 큐의 상태를 검사할 수 있지만, 큐를 정적 배열로 구현하는 경우는 front와 rear 변수가 필요하다.
프로그램 4.2 선형 큐
위 프로그램에서는 리스트를 사용하여 크기가 5인 스택을 생성한다.
파이썬 리스트는 크기 제한이 없지만 예제를 수행하기 위해서 size 변수로 스택의 크기를 지정한다.
원소(3, 4, 5, 6, 7, 8)를 순서대로 추가하면 마지막 원소(8)에서 'stack full'오류가 발생한다.
반대로 pop() 함수를 연속적으로 호출하면 6번째 호출에서 'stack empty' 메세지가 출력된다.
class Queue:
def __init__(self, size) :
self.front = -1
self.rear = -1
self.queue = []
self.size = size
def isEmpty(self) :
return len(self.queue) == 0
def isFull(self) :
return len(self.queue) == self.size
def push(self, item) :
if not self.isFull() :
self.rear += 1
self.queue.append(item)
self.show_queue()
else :
print("Queue full")
def pop(self) :
if not self.isEmpty() :
self.front += 1
return self.queue.pop(0)
else :
print("Queue empty")
def show_queue(self) :
print(self.queue)
q = Queue(5)
for item in [3, 4, 5, 6, 7, 8] :
q.push(item)
for i in range(6) :
q.pop()
q.show_queue()코드를 살펴보았다.
class Queue:
def __init__(self, size) :
self.front = -1
self.rear = -1
self.queue = []
self.size = sizeQueue의 생성자이다.
queue의 front외 rear를 -1로 저장해 큐가 비었음을 알린다.
queue에도 값을 넣지 않는다.
그리고 예제를 수행하기 위해 size를 입력받는다.
def isEmpty(self) :
return len(self.queue) == 0
def isFull(self) :
return len(self.queue) == self.sizeisEmpty() 함수와 isFull 함수를 통해 큐가 비었을 때와 꽉 찼을 때를 판단한다.
비었으면 0을, 꽉 찼으면 size를 반환한다.
def push(self, item) :
if not self.isFull() :
self.rear += 1
self.queue.append(item)
self.show_queue()
else :
print("Queue full")push() 함수를 통해 큐에 값을 입력한다.
만약 Full 상태가 아니라면 맨 뒤를 가리키는 rear의 값을 +1 한 뒤에 item의 값을 queue에 추가하고 show_queue() 함수를 통해 출력한다.
Full 상태라면 Queue full을 출력한다.
def pop(self) :
if not self.isEmpty() :
self.front += 1
return self.queue.pop(0)
else :
print("Queue empty")
def show_queue(self) :
print(self.queue)pop() 함수를 통해 큐의 첫 번째 값을 출력한다.
만약 Empty 상태가 아니라면 맨 앞을 가리키는 front의 값을 +1 한 뒤에 pop(0)을 통해 맨 첫 번째 원소를 출력한다.
Empty 상태라면 Queue empty를 출력한다.
show_queue() 함수를 통해 큐를 출력한다.
q = Queue(5)
for item in [3, 4, 5, 6, 7, 8] :
q.push(item)
for i in range(6) :
q.pop()
q.show_queue()사이즈가 5인 큐 q를 생성한다.
push() 함수를 통해 3, 4, 5, 6, 7, 8의 값을 q에 입력한다.
q의 크기가 5이기 때문에 6번째인 8을 입력할 때 queue full이 출력된다.
pop() 함수를 통해 큐의 첫 번째 원소를 6번 출력한 뒤 삭제하는 것을 반복한다.
q에 저장된 원소가 5개이기 때문에 6번째로 pop을 할 때에는 queue empty가 출력된다.

아래는 큐의 상태를 표로 나타낸 것이다.
|
연산
|
[ 0 1 2 3 4 ]
|
front/rear
|
결과/반환값
|
|
초기상태
|
|
-1/-1
|
|
|
push(3)
|
3
|
-1/0
|
|
|
push(4)
|
3 4
|
-1/1
|
|
|
push(5)
|
3 4 5
|
-1/2
|
|
|
push(6)
|
3 4 5 6
|
-1/3
|
|
|
push(7)
|
3 4 5 6 7
|
-1/4
|
|
|
push(8)
|
3 4 5 6 7
|
-1/4
|
queue full
|
|
pop()
|
4 5 6 7
|
0/4
|
3
|
|
pop()
|
5 6 7
|
1/4
|
4
|
|
pop()
|
6 7
|
2/4
|
5
|
|
pop()
|
7
|
3/4
|
6
|
|
pop()
|
|
4/4
|
7
|
|
pop()
|
4/4
|
queue empty
|
4.3 순환 큐
선형 큐(linear queue) : 원소의 추가, 삭제 시 rear와 front 변수 값이 모두 증가된다.
이 빈도가 증가할수록 원소들이 큐의 오른쪽을 점점 이동하게 되고 왼쪽에는 빈 공간이 생기게 된다.
결국 rear 변수에 의해 가득 찬 큐(queue full) 신호가 발생하더라도 큐 안에 빈 공간이 남아 있을 수 있다.
이런 경우 큐의 빈 공간을 재사용하기 위해서는 원소들을 왼쪽으로 이동시키는 작업(shift)을 주기적으로 해주어야 한다.
위의 예제에서도 큐는 empty 상태이지만 원소를 추가할 수 없다.
위의 예제에서 아래 코드를 추가해서 실행해 보았다.
q.push(10)
print(q.rear)
print(q.front)
q.push(11)
print(q.rear)
print(q.front)
front의 값이 size가 5이 queue의 최대값(4)를 넘은 것을 확인할 수 있다.
파이썬은 동적 배열이고 위의 코드에서 rear과 front를 통해 판단하지 않았기 때문에 코드는 실행되었으나 둘 중 한 가지 조건만 벗어나도 오류가 발생한다.
선형 큐의 이러한 문제점을 개선한 자료구조가 순환 큐(circular queue)이다.
산환 큐의 장점은 큐의 양쪽 끝을 서로 연결하여 원소의 이동 작업 없이 전체 공간을 모두 사용할 수 있다는 점이다.

순환 큐도 마찬가지로 front와 rear 변수가 같으면 빈 큐(empty queue)을 의미한다.
두 변수의 초기값을 모두 0으로 설정한다.
그러나 순환 큐의 공간에 원소가 모두 채워지면 front와 rear 변수의 값이 같아져서 큐의 빈 상태 조건과 구분이 어려워진다.
이를 해결하기 위해서는 최소 1개의 빈 공간을 남겨두거나, 또는 별도의 count 변수를 사용하여 추가된 원소의 개수를 기억해야 한다.
프로그램 4.3 순환 큐
큐의 full과 empty를 구분하기 위해 별도의 count 변수를 사용하여 추가된 원소의 개수를 기억했다.
또한 리스트를 사용하여 고정 크기의 순환 큐를 구현할 때 다음과 같이 None 값으로 미리 큐의 모든 공간을 채워 놓으면 좋다.
None으로 채워 놓지 않으면 원소가 없을 때 리스트의 크기가 자동으로 변경된다.
self.cqueue = [None]*self.size순환 큐는 마지막 공간과 첫 번째 공간이 연결되어 있으므로 변수 값을 변경할 때 다음과 같이 작성하면 된다.
self.rear = (self.rear + 1) % self.size
self.front = (self.front + 1) % self.size순환 큐를 생성하고 원소를 추가 또는 삭제하면서 스택의 상태를 view() 함수를 통하여 단계별로 출력하고 있다.
프로그램의 실행 결과에서 F와 R은 front와 rear 변수를 의미한다.
또한 순환 큐는 full과 empty를 구분하기 위해 더미 공간을 하나 더 추가로 사용한다.
큐의 용량(Capacity)이 4일 경우에 하나 더 추가해 5개의 공간을 사용하는 것이다. ( 0 - 4 인덱스는 큐, 5 인덱스는 더미)
empty일 때는 전단과 후단이 같다는 것을 이용하고 (front = rear)
full일 때는 후단 다음이 전단이라는 사실을 이용한다. (rear → NextNode = front)
자료구조 - 순환 큐(Circular Queue)
큐(Queue)란 먼저 들어간 데이터가 먼저 나오는(FIFO, First In First Out) 자료구조형이다. 스택은 한쪽에서만 데이터를 삽입하고 제거하지만, 큐(Queue)는 데이터를 후단(Back)에서 삽입을(Enqueue) 하고 전
janggom.tistory.com
class CQueue:
def __init__(self, size) :
self.front = 0
self.rear = 0
self.size = size
self.cqueue = [None] * self.size
self.count = 0
def empty(self) :
return self.count == 0
def full(self) :
return self.count == self.size
def view(self) :
print(self.cqueue, 'F = %d R = %d' %(self.front, self.rear))
def push(self, item) :
if not self.full() :
print("Push %2d" %item, end = ' ')
self.rear = (self.rear + 1) % self.size
self.cqueue[self.rear] = item
self.view()
self.count += 1
else :
print("Queue full")
def pop(self) :
if not self.empty() :
print("Pop ", end = ' ')
self.front = (self.front + 1) % self.size
item = self.cqueue[self.front]
self.cqueue[self.front] = None
self.view()
self.count -= 1
return item
else :
print("Queue empty")
q = CQueue(5)
for item in [3, 4, 5] :
q.push(item)
a = q.pop()
q.push(7)
q.push(9)
a = q.pop()
q.push(13)
a = q.pop()
q.push(15)
q.push(8)
q.push(10)
for i in range(6) :
a = q.pop()코드를 살펴보았다.
class CQueue:
def __init__(self, size) :
self.front = 0
self.rear = 0
self.size = size
self.cqueue = [None] * self.size
self.count = 0CQueue의 생성자이다.
front와 rear을 모두 0으로 설정해준다.
이전에는 순환하지 않기 때문에 -1로 설정해도 괜찮았지만 리스트에는 -1이라 함은 뒤에서 첫번째를 가리키기 때문에 0으로 설정해야 한다.
예제를 수행하기 위해 size를 입력받는다.
고정 크기의 순환 큐를 구현하기 위해 리스트를 size만큼 None이 차도록 구현하였다.
그리고 empty와 full을 구분하기 위해 count변수를 0으로 선언하였다.
def empty(self) :
return self.count == 0
def full(self) :
return self.count == self.size
def view(self) :
print(self.cqueue, 'F = %d R = %d' %(self.front, self.rear))empty, full을 나타내는 함수 empty(), full()을 만들었다.
view() 함수로는 cqueue의 값들과 front와 rear을 출력한다.
def push(self, item) :
if not self.full() :
print("Push %2d" %item, end = ' ')
self.rear = (self.rear + 1) % self.size
self.cqueue[self.rear] = item
self.view()
self.count += 1
else :
print("Queue full")push() 함수를 통해서 순환큐에 item을 입력한다.
순환큐가 full이 아니라면 rear+1을 self.size로 나눈 나머지 인덱스의 리스트에 넣는다.
이렇게 하면 size번째 값은 0번째 리스트에, size+1번째 값은 1번째 리스트에 입력하여 순환할 수 있다.
view() 함수를 통해 현재 순환큐를 출력하고 원소의 개수 count에 +1 한다.
순환큐가 full이라면 Queue full을 출력한다.
def pop(self) :
if not self.empty() :
print("Pop ", end = ' ')
self.front = (self.front + 1) % self.size
item = self.cqueue[self.front]
self.cqueue[self.front] = None
self.view()
self.count -= 1
return item
else :
print("Queue empty")pop() 함수를 통해서 순환큐의 첫 번째 원소를 삭제한다.
순환큐가 empty가 아니라면 front+1을 self.size로 나눈 나머지 인덱스의 리스트의 값을 None으로 바꾼다.
이렇게 하면 size번째는 0번째 리스트, size+1번째는 1번째 리스트에 접근하여 순환하며 삭제할 수 있다.
item에 삭제한 값을 넣고 view를 통해 삭제된 순환큐의 모습을 출력한 뒤 원소의 개수 count에 -1 한다.
return item을 통해 필요하다면 삭제된 값을 출력할 수 있도록 했다.
순환큐가 empty라면 Queue empty를 출력한다.
q = CQueue(5)
for item in [3, 4, 5] :
q.push(item)
a = q.pop()
q.push(7)
q.push(9)
a = q.pop()
q.push(13)
a = q.pop()
q.push(15)
q.push(8)
q.push(10)
for i in range(6) :
a = q.pop()크기가 5인 CQueue q를 선언한다.
반복문을 이용해 3, 4, 5를 q에 입력한다.
push()와 pop()을 반복해서 값을 저장한다.
push()를 하면 rear의 값이, pop()을 하면 front의 값이 증가한다.
rear와 front의 값이 같고, count의 값이 0이 아닐 때 stack full을 출력한다.
rear와 front의 값이 같고, count의 값이 0일 때 stack empty를 출력한다.

4.4 순환 데크
데크(Deque : double ended queue) : 큐의 앞(front)와 뒤(rear) 모두에서 원소의 추가와 삭제가 가능한 큐
순환 데크(circular deque) : 데크의 앞과 뒤가 서로 연결된 구조

데크는 기존 선형 큐의 모든 함수 이외에 데크 앞에 원소를 추가하는 함수와 뒤에서 삭제하는 함수가 더 필요하다.
|
데크 함수
|
작업
|
|
add_front()
|
front 위치에 원소 저장 후 front 감소
|
|
del_front()
|
front를 증가시키고 front의 원소 삭제
|
|
add_rear()
|
rear을 증가시키고 원소 저장
|
|
del_rear()
|
rear의 원소를 삭제하고 rear 감소
|
프로그램 4.4 순환 데크
기존 순환 큐 프로그램에 add_front()와 del_rear() 함수가 더 추가되었다.
함수에서 데크의 양 끝 경계를 통과할 때의 계산식에 유의해야 한다.
class CDeque:
def __init__(self, size) :
self.front = 0
self.rear = 0
self.size = size
self.cqueue = [None] * self.size
self.count = 0
def isEmpty(self) :
return self.count == 0
def isFull(self) :
return self.count == self.size
def show_queue(self) :
print(self.cqueue, 'FR', self.front, self.rear)
def add_rear(self, item) :
print("Add Rear %2d" %item, end = ' ')
if not self.isFull() :
self.rear = (self.rear + 1) % self.size
self.cqueue[self.rear] = item
self.show_queue()
self.count += 1
else :
print(" => Deque full")
def add_front(self, item) :
print("Add Front %2d" %item, end = ' ')
if not self.isFull() :
self.cqueue[self.front] = item
self.front = (self.front - 1 + self.size) % self.size
self.show_queue()
self.count += 1
else :
print(" => Deque full")
def del_front(self) :
print("Del Front ", end = ' ')
if not self.isEmpty() :
self.front = (self.front + 1) % self.size
item = self.cqueue[self.front]
self.cqueue[self.front] = None
self.show_queue()
self.count -= 1
return item
else :
print(" => Deque empty")
def del_rear(self) :
print("Del Rear ", end = ' ')
if not self.isEmpty() :
item = self.cqueue[self.rear]
self.cqueue[self.rear] = None
self.rear = (self.rear - 1 + self.size) % self.size
self.show_queue()
self.count -= 1
return item
else :
print(" => Deque empty")
q = CDeque(5)
for item in [17, 20, 6] :
q.add_rear(item)
for item in [3, 4, 5] :
q.add_front(item)
q.del_front()
q.add_front(7)
q.add_rear(9)
q.del_rear()
q.add_front(13)
q.del_rear()
q.add_front(15)
q.add_rear(8)
q.add_rear(10)
for i in range(6) :
a = q.del_rear()코드를 살펴보았다.
class CDeque:
def __init__(self, size) :
self.front = 0
self.rear = 0
self.size = size
self.cqueue = [None] * self.size
self.count = 0CDeque의 생성자이다.
front와 rear을 모두 0으로 설정해주고 size를 매개변수로 입력받는다.
고정 크기의 순환 큐를 구현하기 위해 리스트를 size만큼 None이 차도록 구현하였다.
그리고 empty와 full을 구분하기 위해 count변수를 0으로 선언하였다.
def isEmpty(self) :
return self.count == 0
def isFull(self) :
return self.count == self.size
def show_queue(self) :
print(self.cqueue, 'FR', self.front, self.rear)empty, full을 판단하는 함수 isEmpty(), isFull()을 만들었다.
show_queue() 함수로는 cdeque의 값들과 front와 rear을 출력한다.
def add_rear(self, item) :
print("Add Rear %2d" %item, end = ' ')
if not self.isFull() :
self.rear = (self.rear + 1) % self.size
self.cqueue[self.rear] = item
self.show_queue()
self.count += 1
else :
print(" => Deque full")add_rear() 함수는 rear을 증가시키고 원소를 저장하는 함수이다. 이는 일반 큐에도 있었다. (push()의 역할)
deque에 입력할 원소 item을 출력한 다음, deque가 full이 아니라면 rear + 1번째 인덱스부터 채운다.
show_queue()를 통해 채워진 deque의 모습을 출력한 다음 원소의 개수를 세는 count에 +1 한다.
만약 deque가 full이라면 Deque full을 출력한다.
def add_front(self, item) :
print("Add Front %2d" %item, end = ' ')
if not self.isFull() :
self.cqueue[self.front] = item
self.front = (self.front - 1 + self.size) % self.size
self.show_queue()
self.count += 1
else :
print(" => Deque full")add_front() 함수는 front 위치에 원소를 저장한 후 front를 감소시킨다. 일반 큐에는 없었던 새로운 함수이다.
deque에 입력할 원소 item을 출력한 다음, deque가 full이 아니라면 front 위치에 입력할 원소 item을 저장한다.
front - 1 + size를 통해 front를 1 감소한다.
size를 더하는 이유는 음수가 되지 않도록 순환하게 하기 위해서이다. size보다 값이 커져도 %로 나머지가 계산되니까 문제가 되지 않는다.
show_queue()를 통해 채워진 deque의 모습을 출력한 다음 원소의 개수를 세는 count에 +1 한다.
만약 deque가 full이라면 Deque full을 출력한다.
def del_front(self) :
print("Del Front ", end = ' ')
if not self.isEmpty() :
self.front = (self.front + 1) % self.size
item = self.cqueue[self.front]
self.cqueue[self.front] = None
self.show_queue()
self.count -= 1
return item
else :
print(" => Deque empty")del_front() 함수는 front를 증가시키고 front의 원소를 삭제한다. 이는 일반 큐에도 있었다. (pop()의 역할)
deque가 empty가 아니라면 front를 front + 1번째 인덱스로 바꾸고 그 값을 item에 저장한 다음에 front + 1번째 원소를 삭제한다.
show_queue()를 통해 비워진 deque의 모습을 출력한 다음 원소의 개수를 세는 count에 -1 한다.
만약 deque가 empty이라면 Deque empty를 출력한다.
def del_rear(self) :
print("Del Rear ", end = ' ')
if not self.isEmpty() :
item = self.cqueue[self.rear]
self.cqueue[self.rear] = None
self.rear = (self.rear - 1 + self.size) % self.size
self.show_queue()
self.count -= 1
return item
else :
print(" => Deque empty")del_rear() 함수는 rear의 원소를 삭제하고 rear를 감소시킨다. 일반 큐에는 없었던 새로운 함수이다.
rear번째 원소를 item에 저장하고 삭제한 다음 rear -1 + size를 통해 rear을 1 감소한다.
show_queue()를 통해 비워진 deque의 모습을 출력한 다음 원소의 개수를 세는 count에 -1 한다.
만약 deque가 empty이라면 Deque empty를 출력한다.
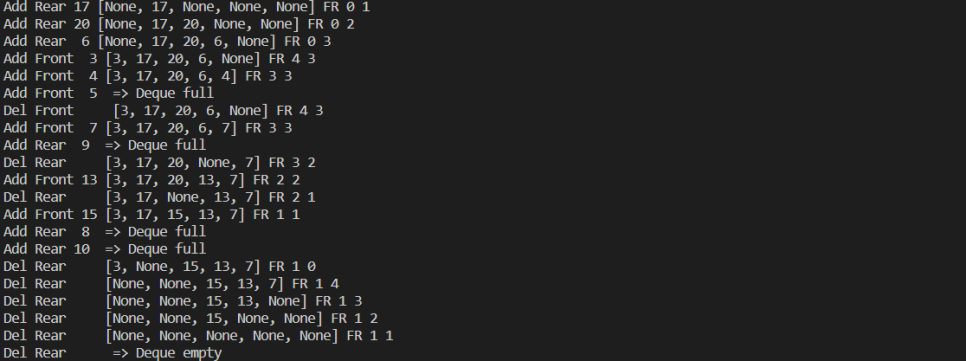
q = CDeque(5)
for item in [17, 20, 6] :
q.add_rear(item)
for item in [3, 4, 5] :
q.add_front(item)
q.del_front()
q.add_front(7)
q.add_rear(9)
q.del_rear()
q.add_front(13)
q.del_rear()
q.add_front(15)
q.add_rear(8)
q.add_rear(10)
for i in range(6) :
a = q.del_rear()이미지로 설명을 대체한다.
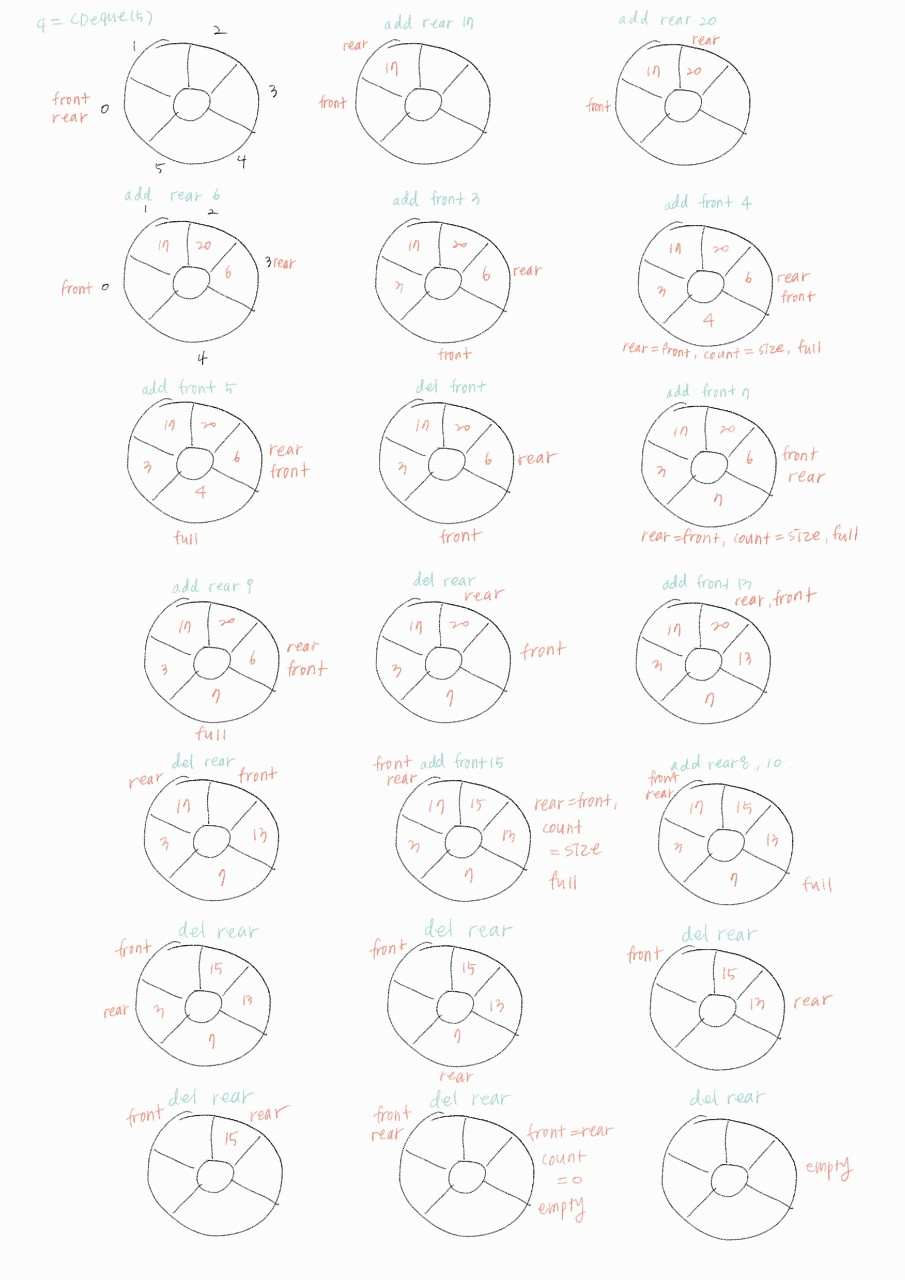
왼 → 오, 위 → 아래 순
add_rear()-del_front() 함수가 일반 큐에 있었음을 기억하고 push()와 pop()에 각각 대응해 기억하면 함수의 역할이 헷갈리지 않을 것이다.
4.5 수식 표현과 평가
수식(expression) = 연산자(operator) + 피연산자(operand)
연산자의 종류에는 산술(arithmetic), 논리(logical), 대입(assignment) 연산자가 있다.
피연산자 위치에는 변수 또는 상수가 올 수 있다.
수식 표기법은 피연산자에 대한 연산자의 위치에 따라 중위 표기법(infix), 후위 표기법(postfix), 전위 표기법(prefix)로 나뉜다.
|
표기법
|
수식의 예
|
|
중위 표기법(infix)
|
a/b-c+d*e-a*c
|
|
후위 표기법(postfix)
|
ab/c-de*+ac*-
|
|
전위 표기법(prefix)
|
-=-/abc*de*ac
|
중위 수식에서 여러 개의 연산자가 함께 존재할 경우 각 연산자의 우선 순위에 따라 순서대로 계산된다.
또한 수식에 우선 순위가 동일한 연산자들이 동시에 존재할 때는 결합성 규칙에 따라 연산 순서가 결정된다.
|
중위 수식(infix)
|
후위 수식(postfix)
|
|
- 순서 : 피연산자 연산자 피연산자
- 각 연산자별로 우선 순위가 있으며, 괄호를 사용하여 우선 순위를 바꿀 수 있다
- 계산 순서가 복잡하다
- 사람이 이해하기는 쉬우나 연산 순서가 복잡하여 프로그래밍이 어렵다
|
- 순서 : 피연산자 피연산자 연산자
- 연산자의 우선 순위가 없고 괄호를 사용하지 않는다
- 왼쪽에서 오른쪽 방향으로 1회 스캔하여 계산하므로 프로그래밍하기 쉽다
- 사람이 직관적으로 이해하기 어렵다
|
|
5+9*7
a*b+c
(2+3)*7
d*e/f
a/(b+c-d)*e*(f-g)
|
597*+
ab*c+
23+7*
de*f/
abc+d-/e*fg-*
|
후위 수식은 연산자가 있으면 무조건 앞의 두 피연산자를 계산한다고 생각하면 쉽다.
프로그램 4.5 후위 수식 계산하기
일반적으로 중위 수식은 구현의 복잡성 때문에 후위 수식으로 먼저 변환한 뒤 계산한다.
먼저, 후위 수식을 스택을 이용하여 계산하는 알고리즘이다.
<후위 수식 평가 알고리즘>
1. 후위 수식(expr)에서 읽은 토큰(token)이 피연산자이면 스택에 넣는다.
2. 토큰이 연산자이면 스택에서 피연산자 2개를 꺼내서 계산한 후 그 결과 값을 다시 스택에 넣는다.
3. 모든 토큰이 입력되면 스택에 마지막으로 저장된 계산값을 꺼내서 반환한다.
후위 수식 57*9+34/-를 계산해 보았다.
|
토큰
|
스택
|
top
|
||
|
[0]
|
[1]
|
[2]
|
||
|
5
|
5
|
|
|
0
|
|
7
|
5
|
7
|
|
1
|
|
*
|
35
|
|
|
0
|
|
9
|
35
|
9
|
|
1
|
|
+
|
44
|
|
|
0
|
|
3
|
44
|
3
|
|
1
|
|
4
|
44
|
3
|
4
|
2
|
|
/
|
44
|
0
|
|
1
|
|
-
|
4
|
|
|
0
|
프로그램 4.5는 2개의 후위 수식에 대해서 eval_postfix() 함수를 호출하여 알고리즘에 의해 계산한다.
getSymtype() 함수는 입력된 토큰(sym)의 유형을 반환한다.
Sym 클래서에 토큰의 유형이 정의되어 있따.
후위 수식의 모든 토큰이 입력되면 스택에 남은 최종 계산값을 반환하고 종료한다.
class Sym :
OPEN_B = 1 # (
CLOSE_B = 2 # )
PLUS = 3 # +
MINUS = 4 # -
TIMES = 5 # *
DIVIDE = 6 # //
MOD = 7 # %
OPERAND = 8 # 피연산자
class Expression :
def __init__(self, expr) :
self.stack = []
self.size = 100
self.expr = expr
self.top = -1
def push(self, item) :
self.top += 1
self.stack.append(item)
self.show_stack()
def pop(self) :
if len(self.stack) > 0 :
self.top -= 1
return self.stack.pop()
else :
print("Stack empty")
def show_stack(self) :
print(self.stack)
def eval_postfix(self) :
for sym in self.expr :
print(sym, end = ' ')
sym_type = self.getSymtype(sym)
if sym_type == Sym.OPERAND :
self.push(int(sym))
else :
op2 = self.pop()
op1 = self.pop()
if sym_type == Sym.PLUS :
self.push(op1 + op2)
elif sym_type == Sym.MINUS :
self.push(op1 - op2)
elif sym_type == Sym.TIMES :
self.push(op1 * op2)
elif sym_type == Sym.DIVIDE :
self.push(op1 // op2)
elif sym_type == Sym.MOD :
self.push(op1 % op2)
return self.pop()
def getSymtype(self, sym) :
if sym == '(' :
sym_type = Sym.OPEN_B
elif sym == ')' :
sym_type = Sym.CLOSE_B
elif sym == '+' :
sym_type = Sym.PLUS
elif sym == '-' :
sym_type = Sym.MINUS
elif sym == '*' :
sym_type = Sym.TIMES
elif sym == '/' :
sym_type = Sym.DIVIDE
elif sym == '%' :
sym_type = Sym.MOD
else :
sym_type = Sym.OPERAND
return sym_type
for expr in ["57*9+34/-", "936+5-/7*64-*"] :
e = Expression(expr)
print("수식 :", expr)
print("결과값 =", e.eval_postfix())
print()코드를 살펴보았다.
class Sym :
OPEN_B = 1 # (
CLOSE_B = 2 # )
PLUS = 3 # +
MINUS = 4 # -
TIMES = 5 # *
DIVIDE = 6 # //
MOD = 7 # %
OPERAND = 8 # 피연산자Sym이라는 토큰을 판단하는 클래스이다.
만약 토큰이 연산자라면 각각의 기호에 번호를 할당했다.
토큰이 피연산자일 경우 전부 스택에 넣을 것이기 때문에 하나로 통일하였다.
class Expression :
def __init__(self, expr) :
self.stack = []
self.size = 100
self.expr = expr
self.top = -1Expression 클래스의 생성자이다.
빈 스택을 생성하고, top을 -1으로 설정한다.
self.expr을 통해 수식을 입력받는다. 수식의 최대 사이즈는 100인데 사용하지 않는 것 같다.
def push(self, item) :
self.top += 1
self.stack.append(item)
self.show_stack()스택에 피연산자를 입력하는 push() 함수이다.
top에 +1 하고 스택에 item을 추가한 뒤 stack을 출력한다.
def pop(self) :
if len(self.stack) > 0 :
self.top -= 1
return self.stack.pop()
else :
print("Stack empty")
def show_stack(self) :
print(self.stack)스택에 있는 피연산자를 출력하는 pop() 함수이다.
len이 0보다 크다는 뜻은 비어 있지 않다는 것이므로 top에서 -1한 뒤에 가장 나중에 들어온 원소를 출력한다.
그렇지 않으면 비어있으므로 Stack empty를 출력한다.
show_stack() 함수를 통해서 stack을 출력한다.
def eval_postfix(self) :
for sym in self.expr :
print(sym, end = ' ')
sym_type = self.getSymtype(sym)
if sym_type == Sym.OPERAND :
self.push(int(sym))
else :
op2 = self.pop()
op1 = self.pop()
if sym_type == Sym.PLUS :
self.push(op1 + op2)
elif sym_type == Sym.MINUS :
self.push(op1 - op2)
elif sym_type == Sym.TIMES :
self.push(op1 * op2)
elif sym_type == Sym.DIVIDE :
self.push(op1 // op2)
elif sym_type == Sym.MOD :
self.push(op1 % op2)
return self.pop()후위 수식을 계산하는 exal_postfix() 함수이다.
수식 expr에 있는 토큰 sym을 하나씩 확인해서 출력한다.
getSymtype(sym) 함수를 통해서 확인하는데, 만약 sym_type이 피연산자라면 int형으로 스택에 push한다.
sym_type이 연산자라면 스택에 있는 피연산자 둘을 pop한 다음 연산자에 맞는 계산을 한 뒤에 다시 스택에 push한다.
토큰을 전부 검사했다면 스택 안에는 결과값만이 있기 때문에 pop을 통해 이를 출력한다.
def getSymtype(self, sym) :
if sym == '(' :
sym_type = Sym.OPEN_B
elif sym == ')' :
sym_type = Sym.CLOSE_B
elif sym == '+' :
sym_type = Sym.PLUS
elif sym == '-' :
sym_type = Sym.MINUS
elif sym == '*' :
sym_type = Sym.TIMES
elif sym == '/' :
sym_type = Sym.DIVIDE
elif sym == '%' :
sym_type = Sym.MOD
else :
sym_type = Sym.OPERAND
return sym_type토큰의 성격을 검사하는 getSymtype() 함수이다.
토큰의 성격에 맞는 값을 할당해 반환한다.
for expr in ["57*9+34/-", "936+5-/7*64-*"] :
e = Expression(expr)
print("수식 :", expr)
print("결과값 =", e.eval_postfix())
print()리스트 안에 있는 수식을 하나씩 Expression class에 넣어 계산하고 수식과 결과값을 출력한다.

프로그램 4.6 중위 수식을 후위 수식으로 바꾸어 계산하기
이번에는 중위 수식(infix)를 후위 수식(postfix)으로 변환하는 알고리즘이다.
수식을 변환하는데 핵심은 중위 수식의 연산자를 우선 순위에 따라 후위 수식의 순서로 재배열하는 것이다.
중위 수식에서는 각 연산자가 위치에 상관없이 우선 순위를 갖지만, 후위 수식은 왼쪽에서 오른쪽으로 이동하면서 만나는 연산자를 먼저 처리한다.
중위 수식을 후위 수식으로 변환할 때 각 연산자는 후위 수식의 올바른 위치를 찾을 때까지 스택에 임시로 보관되어야 한다.
특히, 수식에 괄호가 포함된 경우는 괄호를 연산자로 간주하여 알고리즘에 따라서 처리한다.
<중위 수식을 후위 수식으로 바꾸는 알고리즘>
1. 중위 수식의 토큰이 피연산자이면 그대로 후위 수식으로 출력한다.
2. 토큰이 연산자인 경우는 스택이 비어 있거나, 스택 연산자보다 우선 순위가 높으면 스택에 추가한다.
3. 토큰이 스택 연산자보다 우선 순위가 낮거나 같으면, 스택에서 연산자를 먼저 제거한 후 토큰을 스택에 넣는다.
4. 토큰이 '('이면, 그대로 스택에 추가한다.
5. 토큰이 ')'이면, 스택에서 '('이 나올 때까지 모든 연산자를 제거하여 출력하고 '('은 출력 없이 버린다.
6. 토큰이 문자열 끝(eos)이면, 스택에 남은 모든 연산자를 출력한다.
아래는 중위 수식 a+(b*c+d)*e를 후위 수식으로 변환하는 과정을 나타낸 표이다.
|
토큰
|
출력
|
스택
|
|
a
|
a
|
|
|
+
|
a
|
+
|
|
(
|
a
|
+ (
|
|
b
|
a b
|
+ (
|
|
*
|
a b
|
+ ( *
|
|
c
|
a b c
|
+ ( *
|
|
+
|
a b c *
|
+ ( +
|
|
d
|
a b c * d
|
+ ( +
|
|
)
|
a b c * d +
|
+
|
|
*
|
a b c * d +
|
+ *
|
|
e
|
a b c * d + e
|
+ *
|
|
eos
|
a b c * d + e * +
|
|
이 프로그램은 중위 수식을 후위 수식으로 변환한 후 eval_postfix() 함수에 전달하여 수식의 값을 계산한다.
class Sym :
OPEN_B = 1 # (
CLOSE_B = 2 # )
PLUS = 3 # +
MINUS = 4 # -
TIMES = 5 # *
DIVIDE = 6 # //
MOD = 7 # %
OPERAND = 8 # 피연산자
class Expression :
def __init__(self, expr) :
self.stack = []
self.size = 100
self.expr = expr
self.top = -1
self.output = ""
def push(self, item) :
if not self.isFull() :
self.top += 1
self.stack.append(item)
self.show_stack()
else :
print("Stack full")
def pop(self) :
if not self.isEmpty() :
self.top -= 1
return self.stack.pop()
else :
print("Stack empty")
def isEmpty(self) :
return len(self.stack) == 0
def isFull(self) :
return len(self.stack) == self.size
def show_stack(self) :
print(self.stack)
def eval_postfix(self) :
for sym in self.expr :
print(sym, end = ' ')
sym_type = self.getSymtype(sym)
if sym_type == Sym.OPERAND :
self.push(int(sym))
else :
op2 = self.pop()
op1 = self.pop()
if sym_type == Sym.PLUS :
self.push(op1 + op2)
elif sym_type == Sym.MINUS :
self.push(op1 - op2)
elif sym_type == Sym.TIMES :
self.push(op1 * op2)
elif sym_type == Sym.DIVIDE :
self.push(op1 // op2)
elif sym_type == Sym.MOD :
self.push(op1 % op2)
return self.pop()
def infix_postfix(self) :
for token in expr :
print(token, end = ' ')
if token.isalnum() :
self.output += token
elif token == '(' :
self.push(token)
elif token == ')' :
sym = self.pop()
while sym != '(' :
self.output += sym
sym = self.pop()
else :
while not self.isEmpty() and self.precedence(self.stack[-1]) >= self.precedence(token) :
sym = self.pop()
self.output += sym
self.push(token)
while not self.isEmpty() :
self.output += self.pop()
print()
def precedence(self, op) :
if op == '(' :
return 0
elif op in ['+', '-'] :
return 1
elif op in ['*', '/', '%'] :
return 2
def getSymtype(self, sym) :
if sym == '(' :
sym_type = Sym.OPEN_B
elif sym == ')' :
sym_type = Sym.CLOSE_B
elif sym == '+' :
sym_type = Sym.PLUS
elif sym == '-' :
sym_type = Sym.MINUS
elif sym == '*' :
sym_type = Sym.TIMES
elif sym == '/' :
sym_type = Sym.DIVIDE
elif sym == '%' :
sym_type = Sym.MOD
else :
sym_type = Sym.OPERAND
return sym_type
for expr in ["5*7+(4-3)/6%9", "9/(3+6-5)*7*(6-4)"] :
e = Expression(expr)
print("중위 수식 :", expr)
print()
e.infix_postfix()
print("변환 후위 수식 :", e.output)
e.stack = []
e.expr = e.output
print()
print("후위 수식 계산 값 =", e.eval_postfix())
print()위와 중복되는 코드는 두고 달라지거나 추가된 코드만 살펴보았다.
class Expression :
def __init__(self, expr) :
self.stack = []
self.size = 100
self.expr = expr
self.top = -1
self.output = ""Expression의 생성자이다. 중위 수식을 후위 수식으로 바꾼 뒤 저장할 output이 추가되었다.
def push(self, item) :
if not self.isFull() :
self.top += 1
self.stack.append(item)
self.show_stack()
else :
print("Stack full")
def pop(self) :
if not self.isEmpty() :
self.top -= 1
return self.stack.pop()
else :
print("Stack empty")이전에 push(), pop() 함수를 보다 더 깔끔하게 바꾸었다.
def infix_postfix(self) :
for token in expr :
print(token, end = ' ')
if token.isalnum() :
self.output += token
elif token == '(' :
self.push(token)
elif token == ')' :
sym = self.pop()
while sym != '(' :
self.output += sym
sym = self.pop()
else :
while not self.isEmpty() and self.precedence(self.stack[-1]) >= self.precedence(token) :
sym = self.pop()
self.output += sym
self.push(token)
while not self.isEmpty() :
self.output += self.pop()
print()중위 수식을 후위 수식으로 바꾸는 infix_postfix() 함수이다.
수식 expr에서 토큰을 하나씩 받아와서 만약 토큰이 숫자거나 알파벳이면, 즉 피연산자이면 output에 그대로 추가한다.
만약 토큰이 '('라면 일단 push를 한다.
그리고 토큰이 ')'라면 일단 계산에 포함되지 않는 괄호는 삭제하고 '('가 나올 때까지 연산자인 토큰을 output에 추가한다.
괄호 사이에 들어가지 않는 연산자는 이미 스택에 들어가있는 연산자와 비교해서 우선 순위가 낮거나 같다면 연산자를 제거한 뒤 스택에 넣는다.
우선 순위가 높다면 그냥 스택에 넣는다.
토큰을 다 확인했다면 스택에 들어있는 연산자를 전부 후위 수식에 추가한다.
def precedence(self, op) :
if op == '(' :
return 0
elif op in ['+', '-'] :
return 1
elif op in ['*', '/', '%'] :
return 2precedence() 함수는 중위 수식을 후위 수식으로 변환할 때의 연산자의 우선순위를 확인하는 함수이다.
( << +, - << * / % 순서이다.




