| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- acc
- beebox
- backjoon
- System
- 와이어샤크
- bWAPP
- Reflected
- pwnable
- Systemhacking
- basicrce3
- cloud
- datastructure
- CodeEngn
- 유석종교수님
- AWS
- cgroup
- Linux
- EC2
- c
- wireshark
- 백준
- SISS
- htmlinjection
- python
- mount
- Dreamhack
- Reversing
- fork-bomb
- 자료구조
- grafana
- Today
- Total
Ctrl + Shift + ESC
CHAPTER 03 재귀 호출 본문
3.1 재귀 호출의 개념
재귀 호출(recursion) : 함수의 실행 중에 자신을 다시 호출하는 상황
동일한 함수가 다시 호출되어 혼동될 수 있지만 시스템 입장에서는 또 다른 함수가 불리는 것과 같다.
함수가 실행되면 함수의 실행 환경 정보(컨텍스트)가 저장된 활성 레코드가 생성되어 시스템 스택에 추가된다.
함수의 컨텍스트에는 지역 변수, 복귀 주소 등이 포함된다.
따라서 재귀 함수는 호출되는 횟수만큼 활성 레코드가 스택에 쌓이게 된다.
프로그램 3.1 재귀문 팩토리얼
이전 프로그램 2.2에서 팩토리얼 함수를 다뤘었다.
반복문 팩토리얼 함수를 재귀문으로 변환하여 작성했다.
프로그램 3.1은 재귀 함수로 10 ~ 20까지의 팩토리얼을 각각 계산하는 프로그램이다.
예를 들어 fact(4)를 호출하면 연속적으로 하위 팩토리얼 함수가 재귀 호출된다. (fact(3), fact(2), fact(1)…)
fact(0)에 도달하면 1이 반환되고 더 이상 재귀 호출되지 않는다.
재귀 호출을 멈추는 조건을 종결 조건(exit condition)이라고 한다.
종결 조건을 잘못 설정하면 무한 루프에 빠질 수 있으니 주의해야 한다.
def fact(n) :
if n == 0 :
return 1
else :
return n * fact(n-1)
i = 20
for n in range(10, i+1) :
print(n, "!=", fact(n))
프로그램 3.2 최대 공약수
프로그램 1.3 분수 연산과 출력하기에서 분수를 약분하기 위해 최대공약수를 구한 바 있었다.
이를 응용해서 재귀 함수를 이용해서 최대 공약수를 구하는 예제를 작성했다.
gdc(128, 12)의 원리를 정리해 보자면
gcd(128, 12) = gcd(12, 128 % 12) = gcd(12, 8) = gcd(8, 12 % 8) = gcd(8, 4) = gcd(4, 8 % 4) = gcd(4, 0) = 4
의 과정을 거친다.
def gcd(x, y) :
if y == 0 :
return x
else :
return gcd(y, x % y)
num = [(128, 12), (45, 120)]
for x, y in num :
print("gcd( %d, %d ) = %d" % (x, y, gcd(x, y)))
개인적으로는 반복문을 사용한 이 코드가 깔끔해서 좋아하는 편이다.
def gcd(a, b):
while a % b != 0:
a, b = b, a % b
return b
3.2 이진 탐색
순차 탐색(sequential search)은 원하는 원소를 찾을 때까지 순서대로 반복 비교를 수행한다.
이 방법은 정렬 과정 없이 바로 탐색을 수행할 수는 있으나 탐색 성능 편차가 큰 단점이 있다.
이진 탐색(binary search)은 순차 탐색과 달리 탐색 대상을 미리 정렬해 두어야 한다.
그 이유는 정렬된 리스트에서 중간 값(median)과 비교하기 때문이다.
<반복문 이진 탐색 알고리즘>
1. 탐색 범위에 원소가 없으면 종료하고, 원소가 있으면 리스트의 중간 값(median)과 탐색 키(search key)를 비교한다.
2. 탐색 키가 중간 값과 일치하면 그 위치를 반환하고 탐색을 종료한다.
3. 탐색 키가 중간 값보다 작으면 중간 값의 왼쪽 서브 리스트를 탐색 범위로 변경하여 1번부터 반복한다.
4. 탐색 키가 중간 값보다 크면 중간 값의 오른쪽 서브 리스트를 탐색 범위로 변경하여 1번부터 반복한다.
중간 값과 비교하여 탐색에 성공하면 알고리즘을 종료한다.
탐색 키가 중간 값보다 작으면 중간 값의 왼쪽 서브 리스트가 새로운 탐색 범위로 변경된다.
탐색 키가 중간 값보다 크면 오른쪽 서브 리스트가 탐색 범위가 된다.
이 과정을 반복하여 탐색에 성공하거나, 탐색 범위에 비교할 원소가 없으면 알고리즘을 종료한다.
이진 탐색은 사전 정렬이라는 조건이 필요하지만 탐색 효율이 O(logn)으로 뛰어난 편이다.
순차 탐색과 이진 탐색의 시간 비교를 해보았다.
조건은 동일하게 반복문으로 하고 코드는 뒤에 나오는 코드를 살짝 개량했다.
개수가 적어서 시간의 차이가 잘 보이지 않길래 개수도 늘려보았고 랜덤으로 넣어보았다.
import time
import random
def binary_search(lst, item, left, right) :
while left <= right :
mid = (left + right) // 2
if item == lst[mid] :
return mid
else :
if item < lst[mid] :
right = mid - 1
else :
left = mid + 1
return -1
def sequential_search(lst, item) :
for i in range(len(lst)) :
if item == lst[i] :
return i
return -1
mylist = []
for i in range(70) :
num = random.randint(1, 500)
mylist.append(num)
mylist.sort()
print("binary_search")
time1 = time.time()
for item in [60, 9, 108] :
pos = binary_search(mylist, item, 0, len(mylist)-1)
print("position of %2d = %2d" % (item, pos))
time2 = time.time()
print("time = ", time2 - time1)
print("sequential_search")
time1 = time.time()
for item in [60, 9, 108] :
pos = sequential_search(mylist, item)
print("position of %2d = %2d" % (item, pos))
time2 = time.time()
print("time = ", time2 - time1)
시간 차이가 꽤 나는 것은 아니지만 확실히 나는 것을 확인할 수 있다.
프로그램 3.3 반복문 이진 탐색
해당 프로그램은 반복문으로 구현된 이진 탐색 알고리즘이다.
정렬된 리스트에서 [60, 9, 10] 원소를 각각 이진 탐색한다.
60과 9는 탐색에 성공하여 리스트 상의 위치(인덱스)가 출력되고, 10은 탐색에 실패하여 -1이 출력된다.
# 반복문 이진 탐색
def binary_search(lst, item, left, right) :
while left <= right :
mid = (left + right) // 2
if item == lst[mid] :
return mid
else :
if item < lst[mid] :
right = mid - 1
else :
left = mid + 1
return -1
mylist = [5, 8, 9, 11, 13, 17, 23, 32, 45, 52, 60, 72]
print(mylist)
for item in [60, 9, 10] :
pos = binary_search(mylist, item, 0, len(mylist)-1)
print("position of %2d = %2d" % (item, pos))
프로그램 3.4 재귀문 이진 탐색
해당 프로그램은 재귀문으로 재작성한 이진 탐색 프로그램이다.
원리는 반복문 함수와 동일하나 각 서브 리스트를 재탐색하는 부분을 재귀 함수 호출로 처리하고 있다.
재귀 함수 호출 시마다 탐색 범위가 변경되며, 범위 내에서 탐색 키를 발견하거나 비교할 원소가 없으면 종료된다.
# 재귀문 이진 탐색
def rbinsearch(lst, item, left, right) :
while left <= right :
mid = (left + right) // 2
if item == lst[mid] :
return mid
elif item < lst[mid] :
return rbinsearch(mylist, item, left, mid-1)
else :
return rbinsearch(mylist, item, mid+1, right)
return -1
mylist = [5, 8, 9, 11, 13, 17, 23, 32, 45, 52, 60, 72]
print(mylist)
for item in [60, 9, 10] :
pos = rbinsearch(mylist, item, 0, len(mylist)-1)
print("position of %2d = %2d" % (item, pos))
3.3 피보나치 수열
피보나치 수열은 이전 두 개의 값의 합으로 다음 값을 계산하는 수열이다.
이전 프로그램 1.1에서 다룬 바가 있다.
프로그램 3.5 피보나치 수열
아래 프로그램에는 재귀문으로 피보나치 수열을 구하는 두 종류의 함수가 포함되어 있다.
첫 번째 함수(fibo1)는 피보나치 수를 계산할 때마다 이전 수를 구하기 위해 다시 피보나치 함수를 호출한다.
이 방식은 피보나치 수가 클수록 재귀 호출 횟수가 급격히 증가한다.
반면 두 번째 함수(fibo2)는 마찬가지로 재귀 호출을 사용하지만 이전에 구한 피보나치 수를 함께 반환하여 함수를 중복 호출하지 않는다.
코드를 살펴보았다.
# 피보나치 수열
import time
def fibo1(n) :
global count1
count1 += 1
if n <= 1 :
return n
else :
return fibo1(n-2) + fibo1(n-1)
def fibo2(n) :
global count2
count2 += 1
if n <= 1 :
return (0, n)
else :
(a, b) = fibo2(n-1)
return (b, a+b)
for num_max in [10, 20, 30, 40] :
count1 = 0
count2 = 0
f = []
print("fibo1", num_max)
time1 = time.time()
for d in range(num_max) :
f.append(fibo1(d))
time2 = time.time()
print("time1 =", time2 - time1)
print("recursion1 = ", count1, 'for F%d' %num_max)
print()
time1 = time.time()
print("fibo2", num_max, "=", fibo2(num_max))
time2 = time.time()
print("time2 =", time2 - time1)
print("recursion2 = ", count2)
print(f)
print()코드를 자세히 살펴보았다.
def fibo1(n) :
global count1
count1 += 1
if n <= 1 :
return n
else :
return fibo1(n-2) + fibo1(n-1)매번 재귀 호출을 하는 fibo1() 함수이다.
fibo1() 함수를 실행한 경우를 세기 위한 변수 count를 global로 지정해 함수가 끝난 뒤에도 값이 지속되게 한다.
fibo1() 함수가 실행될 때마다 count1에 1씩 더한다.
fibo1 () 함수가 재귀적으로 실행되어 1보다 작은 수가 호출되면 n을 그대로 반환하고, 그렇지 않으면 fibo1(n-2)와 fibo1(n-1)을 불러온다.
해당 함수는 하나의 fibo 값을 불러오기 위해 2개의 fibo 값을 불러와야 한다.
이 값은 n이 커질 수록 기하급수적으로 늘어난다. (각각의 fibo 함수도 값을 구할 때 다른 fibo 함수를 불러오기 때문이다.)
def fibo2(n) :
global count2
count2 += 1
if n <= 1 :
return (0, n)
else :
(a, b) = fibo2(n-1)
return (b, a+b)이전에 구한 피보나치 수를 함께 반환하는 fibo2() 함수이다.
fibo 2() 함수도 마찬가지로 count를 global로 지정하고 실행될 때마다 1씩 더한다.
값을 튜플로 반환하고, 함수 안에 함수를 입력하되 이전 값을 튜플로 받기 때문에 위의 함수처럼 함수를 반복 호출할 필요가 없다.
for num_max in [10, 20, 30, 40] :
count1 = 0
count2 = 0
f = []
print("fibo1", num_max)
time1 = time.time()
for d in range(num_max) :
f.append(fibo1(d))
time2 = time.time()
print("time1 =", time2 - time1)
print("recursion1 = ", count1, 'for F%d' %num_max)
print()본 함수이다.
구하고자 하는 fibo의 값을 10, 20, 30, 40으로 지정했다. (40은 컴퓨터 여건이 되지 않아서 실행하지 못했다.)
각 횟수를 셀 count를 초기화하고, 피보나치 값을 저장할 함수 f를 빈 리스트로 생성한다.
time1과 time2의 시간 차이로 fibo1() 함수가 실행되는 시간을 측정한다.
실행된 횟수 count1도 함께 출력한다.
fibo2는 튜플로 값을 반환하기 때문에 fibo1에서 리스트에 반환값을 저장해 피보나치 함수 값을 출력한다. (후에)
time1 = time.time()
print("fibo2", num_max, "=", fibo2(num_max))
time2 = time.time()
print("time2 =", time2 - time1)
print("recursion2 = ", count2)
print(f)
print()역시 time과 count로 횟수를 비교한다.

원래는 40의 값도 살펴보려 했으나 노트북의 한계로 40은 값이 출력되는데 5분 이상 걸려서 넘겼다.
두 가지 함수를 이용하여 피보나치 수를 계산하는데 걸리는 시간(교수님 기준)과 재귀 호출 횟수를 비교한 결과이다.
중복된 호출이 없는 fibo2() 함수의 경우가 훨씬 효율적인 것을 알 수 있다.
특히 F40을 계산하는데 fibo1() 함수는 71.5초의 시간이 소요되고 약 5억 3천번의 재귀 호출이 발생한다.
|
피보나치 수
|
재귀 함수
|
소요 시간(초)
|
재귀 호출 횟수
|
|
10
|
fibo1
|
0
|
276
|
|
fibo 2
|
0
|
10
|
|
|
20
|
fibo1
|
0.005
|
35400
|
|
fibo 2
|
0
|
20
|
|
|
30
|
fibo1
|
0.581
|
4356586
|
|
fibo 2
|
0.0009
|
30
|
|
|
40
|
fibo1
|
71.5
|
535828550
|
|
fibo 2
|
0.0
|
40
|
3.4 하노이 타워
하노이 타워(Tower of Hanoi) : 3개의 기둥과 크기가 서로 다른 원반들이 존재할 때, 한 기둥에 꽂힌 원반들을 그대로 다른 기둥으로 옮기는 문제
원반을 움직일 때는 다음의 조건을 만족해야 한다.
1. 한 번에 하나의 원반만 옮길 수 있다.
2. 큰 원반이 작은 원반 위에 놓일 수 없다.
프로그램 3.6 하노이 타워
하노이 타워 문제는 재귀 호출을 이용하여 쉽게 풀 수 있다.
<하노이 타워 알고리즘>
세 개의 기둥(A, B, C)이 있고 기둥 A에서 B로 n개의 원반을 옮긴다고 가정할 때,
1. 기둥 A에서 n-1개의 원반을 A, B가 아닌 기둥 C로 옮긴다.
2. 기둥 A에 남은 1개의 원반을 B로 옮긴다.
3. 기둥 C에 있는 n-1개를 B로 옮긴다.
알고리즘에서 1번과 3번 과정은 원반의 수가 1개 줄어든 또 다른 하노이 타워 문제이므로 재귀적으로 해결할 수 있다.
# 하노이 타워
def htower(n, a, b) :
global count
count += 1
if n == 1 :
print("Disc %d, moved from Pole (%d) to (%d)" % (n, a, b))
else :
c = 6 - a - b # 비어 있는 기둥
htower(n-1, a, c)
print("Disc %d, moved from Pole (%d) to (%d)" % (n, a, b))
htower(n-1, c, b)
count = 0
n = int(input("Enter disc number :" ))
htower(n, 1, 2)
print("# move for %d discs : %d" % (n, count))코드를 자세히 살펴보았다.
c = 6 - a - b # 비어 있는 기둥하노이 타워 코드이다.
위에서 말했듯이 하노이 타워 코드는 n-1개의 원반을 가진 또 다른 하노이 타워 코드로 재귀적인 호출을 통해 해결할 수 있다.
기둥은 1번, 2번, 3번으로 총 3개의 기둥이 있다.
따라서 6( = 3 + 2 + 1) - a(3, 2, 1 중 하나의 기둥) - b(3, 2, 1 중 하나의 기둥) 을 통해 빈 기둥을 알아낼 수 있다.
htower(n-1, a, c)
print("Disc %d, moved from Pole (%d) to (%d)" % (n, a, b))
htower(n-1, c, b)아까 생각했던 알고리즘 1을 수행하는 코드이다. (비어 있는 기둥 C로 n-1개의 원반을 옮기기)
if n == 1 :
print("Disc %d, moved from Pole (%d) to (%d)" % (n, a, b))알고리즘 2를 수행하는 코드이다. (기둥 A에 남은 1개의 원반을 B로 옮기기)
htower(n-1, c, b)알고리즘 3을 수행하는 코드이다. (기둥 C에 있는 n-1개의 원반을 B로 옮기기)
어쩌면 하노이 타워의 조건 2(큰 원반이 작은 원반 위에 놓일 수 없다) 때문에 해당 알고리즘이 어색하게 느껴질 수 있다.
하지만 알고리즘 1에서 비어 있는 기둥 C로 옮기는 과정에서 재귀적인 호출을 부른다.
지금 크게는 디스크가 3개인 하노이 타워를 풀고 있지만 재귀 호출을 통해 디스크가 1개인 하노이 타워 문제로 쪼갠 것이다.
디스크가 1개인 하노이 타워는 고민할 필요가 없다. 바로 옆의 기둥으로 옮기면 되니까!
그래서 각 재귀 호출도 결국 if n == 1 : 에 닿게 되고
하노이 타워(디스크 1개) → 하노이 타워 (디스크 2개) → 하노이 타워 (디스크 3개) 의 순차적으로 풀게 된다.


3개의 원반을 이동시킬 경우 총 7번의 원반 이동이 필요하고, 4개의 원반을 이동시키는 경우 15번의 이동 횟수가 필요하다.
이 알고리즘은 원반의 개수가 n개일 때 (2^n) -1 번의 이동이 필요하므로 시간 복잡도는 지수함수 O(2^n)이 된다.
지수 함수 시간 복잡도는 n이 조금만 커져도 프로그램의 수행 시간이 급격히 증가하므로 주의해야 한다.
3.5 미로 탈출
이번에는 미로에 갇힌 로봇을 탈출시키는 문제를 재귀적 방법으로 해결해 보자.
미로는 다음과 같이 0과 1의 값으로 된 10행 10열의 2차원 배열에 표현되어 있다.
0은 갈 수 있는 길이고 1은 벽으로 막힌 길이다.
현재 로봇은 좌표 (1, 1)에 있으며, 전후 좌우 직선으로만 움직일 수 있고 대각선으로는 갈 수 없다.
미로에서 'X'로 표시된 지점에 도착하면 탈출 성공으로 판단한다.
프로그램 3.7 미로 탈출
<미로 탈출 알고리즘>
1. 현재 위치(P)에서 주변 4 방향(N, E, S, W)을 순서대로 검사하여 갈 수 있는(벽이 아닌 미 방문) 위치(P)를 찾는다.
2. 갈 수 있는 위치(N)가 '탈출구(X)'이면 '탈출 성공'으로 처리하고 종료한다.
3. 갈 수 있는 위치(N)가 '탈출구(x)'가 아니면 현재 위치(P)를 경로 리스트에 저장하고, 새 위치(N)로 탐색 위치를 변경한 후 탐색 함수를 재귀 호출한다.
4. 현재 위치(P) 주변에 갈 수 있는 방향이 없으면 위치(P)를 경로 리스트에서 삭제하고 이전 위치로 되돌아가서, 아직 탐색하지 않은 방향이 있으면 탐색을 재개한다.
5. 더 이상 되돌아 갈 곳이 없고, 탐색할 방향이 없으면 '탈출 실패'로 처리하고 종료한다.
이 프로그램의 시간 복잡도는 미로의 크기인 O(row*col)에 비례한다.
# 미로 탈출
class Maze :
def __init__(self) :
self.maze = [[1, 1, 1, 1, 1, 1, 1, 1, 1, 1], \
[1, 0, 0, 1, 0, 0, 0, 0, 1, 1], \
[1, 1, 0, 1, 0, 1, 1, 0, 0, 1], \
[1, 0, 0, 0, 0, 1, 1, 1, 1, 1], \
[1, 0, 1, 1, 0, 1, 0, 0, 0, 1], \
[1, 0, 0, 1, 0, 1, 1, 0, 1, 1], \
[1, 1, 0, 0, 1, 0, 0, 0, 1, 1], \
[1, 1, 1, 0, 0, 0, 1, 0, 0, 1], \
[1, 0, 0, 0, 1, 0, 1, 1, 'X', 1], \
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1]]
self.mark = [[0]*10 for i in range(10)]
self.path = []
self.found = False
def empty(self) :
return len(self.pah) == 0
def add(self, row, col) :
self.path.append((row, col))
def delete(self) :
return self.path.pop()
def view(self) :
print("path", self.path)
def rexplore(self, row, col) :
for x, y in [(0,-1), (1,0), (0,1), (-1,0)] :
next_col = col + x
next_row = row + y
if self.maze[next_row][next_col] == 'X' :
self.add(row, col)
self.add(next_row, next_col)
self.found = True
return True
elif self.maze[next_row][next_col] == 0 and self.mark[next_row][next_col] == 0 :
self.mark[next_row][next_col] = 1
if (row, col) not in self.path :
self.add(row, col)
result = self.rexplore(next_row, next_col)
if result :
return True
else :
self.delete()
return False
m = Maze()
m.found = m.rexplore(1, 1)
if not m.found :
print("탈출 경로 없음")
else :
print("탈출 성공 : ")
m.view()코드를 살펴보았다.
def __init__(self) :
self.maze = [[1, 1, 1, 1, 1, 1, 1, 1, 1, 1], \
[1, 0, 0, 1, 0, 0, 0, 0, 1, 1], \
[1, 1, 0, 1, 0, 1, 1, 0, 0, 1], \
[1, 0, 0, 0, 0, 1, 1, 1, 1, 1], \
[1, 0, 1, 1, 0, 1, 0, 0, 0, 1], \
[1, 0, 0, 1, 0, 1, 1, 0, 1, 1], \
[1, 1, 0, 0, 1, 0, 0, 0, 1, 1], \
[1, 1, 1, 0, 0, 0, 1, 0, 0, 1], \
[1, 0, 0, 0, 1, 0, 1, 1, 'X', 1], \
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1]]
self.mark = [[0]*10 for i in range(10)]
self.path = []
self.found = Falsemaze 함수의 생성자이다.
self.maze라는 미로를 만든다.
그리고 self.mark라는 0으로 채워진 미로 사이즈의 2차원 리스트를 만들어 중복된 경로를 거치지 않도록 한다.
self.path라는 이동 경로를 저장할 배열과 self.found라는 flag의 기능을 하는 boolean 변수도 만든다.
def empty(self) :
return len(self.path) == 0
def add(self, row, col) :
self.path.append((row, col))
def delete(self) :
return self.path.pop()
def view(self) :
print("path", self.path)empty라는 self.path의 길이를 0으로 리턴하는 함수를 만들었다. 사용이 되나...?
add 함수는 self.path 리스트에 입력된 (row, col)을 추가한다.
delete 함수는 현재 self.path의 마지막 원소를 제거한다.
view 함수는 self.path 리스트를 출력한다.
def rexplore(self, row, col) :
for x, y in [(0,-1), (1,0), (0,1), (-1,0)] :
next_col = col + x
next_row = row + yrexplore 함수이다.
여기서 (0,-1), (1,0), (0,1), (-1,0)의 네 가지 값이 주어지는데 각각 N, E, S, W로 이동했을 때 변동되는 값이다.
변한 값을 적용해서 next_col과 next_row에 입력한다.
if self.maze[next_row][next_col] == 'X' :
self.add(row, col)
self.add(next_row, next_col)
self.found = True
return True만약 미로에서 다음으로 이동한 값이 X, 즉 목적지라면
add 함수를 통해서 (row, col)과 (next_row, next_col) 값을 path에 추가한다.
그 뒤 self.found를 True로 바꾸어서 미로를 탈출했음을 알린다.
더 이상 재귀함수를 통해 목적지를 찾을 필요가 없어졌기 때문에 return True를 통해 함수를 멈추고 목적지를 찾았음을 알린다.
elif self.maze[next_row][next_col] == 0 and self.mark[next_row][next_col] == 0 :
self.mark[next_row][next_col] = 1
if (row, col) not in self.path :
self.add(row, col)
result = self.rexplore(next_row, next_col)
if result :
return True
else :
self.delete()
return False그렇지 않고 이동한 경로가 0이고, 그 경로가 이동하지 않은 곳이었을 때
self.mark를 1로 바꾸어 해당 위치를 지나갔음을 알린다.
그리고 (row, col)를 경로에 추가한 뒤 result를 이용해 재귀함수로 nexw_row, next_col의 위치부터 다시 탐색하도록 한다.
만약 result가 true라면 위에서 본 목적지를 찾은 경우이므로 이전 함수들도 전부 True를 반환하여 재귀를 끝내도록 한다.
그렇지 않으면 해당 경로를 지우고 다른 경로로 갈 수 있도록 delete 함수를 이용해 이동 경로를 지운다.
사방으로 이동해 보았으나 다 막혔을 때에는 이동 경로가 없기 때문에 return False로 재귀를 마친다.
m = Maze()
m.found = m.rexplore(1, 1)
if not m.found :
print("탈출 경로 없음")
else :
print("탈출 성공 : ")
m.view()m이라는 미로를 만들어서 m.found를 (1, 1)에서부터 시작한다.
만약 (1,1)로부터 "X"를 찾지 못했다면 탈출 경로 없음을 출력하고, 찾았다면 탈출 성공을 출력한 뒤에 탈출 경로를 출력한다.
3.6 N-Queens 문제
체스에서 퀸은 가로, 세로, 대각선으로 마음대로 이동할 수 있는 기물이다.
N-Queens 문제는 N개의 퀸이 서로 공격하지 않도록 N*N 체스판에 놓을 수 있는 위치를 찾는 문제이다.
N이 커질수록 경우의 수가 증가하여 해를 찾는데 많은 시간이 걸리게 된다.
<N-Queens 문제 조건>
- 퀸은 가로, 세로, 대각선으로 자유롭게 이동할 수 있다.
- 서로 공격하지 않도록 각 행과 각 열에 한 개의 퀸을 놓아야 한다.
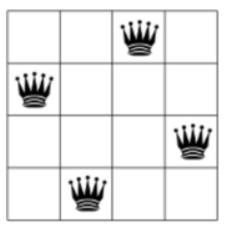
이것을 8-Queens 문제로 확장해 보자.
8-Queens 문제에서 배치할 수 있는 경우의 수는 64개의 체스 칸에서 8개의 위치를 찾는 문제이므로, 다음과 같이 조합 공식 C(64,8)로 계산할 수 있다. 이 방식에서 가능한 경우의 수는 44억개가 넘는다.

이 문제를 다음과 같이 순열의 문제로 변형하면 경우의 수를 줄일 수 있다.
즉, 각 행에 1개의 퀸을 놓을 수 있으므로 각 행의 어느 열에 놓을지만 결정하면 된다.
따라서 이 때 경우의 수는 8! = 40,320과 같이 순열을 구하는 문제와 동일하다.
따라서, N-Queens 문제의 시간 복잡도는 O(N!)이라고 할 수 있다.
여기서 N은 퀸(또는 행)의 수이다.
다음의 8-Queens 문제의 해 중 하나이다.

백트래킹(backtracking) 알고리즘 : 주어진 문제의 해를 구하기 위한 모든 가능한 경우를 나열하여 하나씩 시도하는 알고리즘
더 이상 해에 도달할 가능성이 없는 하위 경우는 제외하여 경우의 수를 줄이고, 그 다음 경우로 되돌아가서 시도하는 방법이다.
위에서 작성했던 미로 탈출 코드도 백트래킹 알고리즘에 해당한다.

위의 사진은 4-Queens 문제의 해를 백트래킹 방법으로 찾는 과정이다.
아래 그림은 4-Queens 문제를 백트래킹 알고리즘으로 해결하는 과정을 트리로 나타낸 것이다.
특정 단계에서 실패하면 그 하위 단계는 모두 제외되고 다음 단계로 넘어간다.

아래 표는 N-Queens 문제에서 유일 해(unique solution)의 개수를 정리한 표이다.
유일 해란 서로 대칭인 경우를 제외한 해를 의미한다.
해의 수는 N!로 증가한다.
|
N
|
유일 해
|
|
1
|
1
|
|
2
|
0
|
|
3
|
0
|
|
4
|
1
|
|
5
|
2
|
|
6
|
1
|
|
7
|
6
|
|
8
|
12
|
|
9
|
46
|
|
10
|
92
|
프로그램 3.8 N-Queens 문제
다음 프로그램은 N-Queens 문제의 해를 재귀적으로 구하는 프로그램이다.
put_queen(0)으로 프로그램이 시작되고 각 행에서 퀸을 놓을 수 있는 열의 위치를 탐색한다.
check_pos() 함수는 현재 위치(row, col)에 퀸을 놓을 수 있는지 이전 행에 놓은 퀸의 위치와 비교하여 검사한다.
마지막 행까지 퀸을 무사히 놓으면 해를 찾은 체스 보드를 출력한다.
N = 6일 때 4개의 정답이 출력되었다.
이 결과는 대칭인 경우를 포함한 것으로 유일 해는 1개이다.
class NQueens:
def __init__(self, size):
self.size = size
self.solutions = 0
self.col = [-1] * size
def solve(self):
self.put_queen(0)
print("Found", self.solutions, "solutions.")
def put_queen(self, row):
if row == self.size:
self.show_board()
self.solutions += 1
else:
for col in range(self.size):
if self.check_pos(row, col):
self.col[row] = col
self.put_queen(row + 1)
def check_pos(self, rows, col):
for i in range(rows):
if self.col[i] == col or \
self.col[i] - i == col - rows or \
self.col[i] + i == col + rows:
return False
return True
def show_board(self):
for row in range(self.size):
line = ""
for column in range(self.size):
if self.col[row] == column:
line += "Q "
else:
line += "+ "
print(line)
print("\n")
N = 6
q = NQueens(N)
q.solve()코드를 자세히 살펴보자
class NQueens:
def __init__(self, size):
self.size = size
self.solutions = 0
self.col = [-1] * sizeNQueens 코드의 생성자이다.
size를 입력받아 self.size에 넣고 solutions의 갯수를 0으로 초기화한다.
그리고 column 값을 넣을 self.column에 -1값을 넣어 size만큼 만든다.
해당 리스트는 row행의 col값을 저장하는 역할을 하는데, 0행부터 시작하기 때문에 값이 겹치지 않기 위해 -1을 입력했다.
def solve(self) :
self.put_queen(0)
print("Found", self.solutions, "solutions.")solve() 함수이다.
put_queen() 함수에 0을 대입한다.
이는 (0, 0)부터 퀸을 놓는다는 뜻이다.
put_queen() 함수에서 해를 구하면 solve에서 답을 출력한다.
def put_queen(self, row):
if row == self.size:
self.show_board()
self.solutions += 1
else:
for col in range(self.size):
if self.check_pos(row, col):
self.col[row] = col
self.put_queen(row + 1)put queen() 함수이다.
row의 값을 매개변수로 받는다. 처음에는 0을 입력받은 뒤 1씩 증가시킨다.
만약 row의 값이 size와 같다면, 즉 마지막 행까지 문제 없이 구해졌다면 답을 구한 것이기 때문에 해당 형태를 show_board() 함수를 통해서 출력하고, solution의 값에 +1을 한다.
마지막 행까지 도달하지 못했다면 해당 행 (0, 1, 2…)의 열을 반복문을 이용해서 0부터 size(끝)까지 반복문과 check_pos() 함수를 이용해서 퀸을 놓아도 되는 자리인지 확인한다.
퀸을 놓아도 되는 자리라면 해당 열의 값을 col[row]에 입력하고, 다음 행으로 넘어간다.
def check_pos(self, rows, col):
for i in range(rows):
if self.col[i] == col or \
self.col[i] - i == col - rows or \
self.col[i] + i == col + rows:
return False
return Truecheck_pos() 함수이다.
row와 col 값을 매개변수로 입력받아 row(행)의 값만큼 반복한다.
참고로 가로 값은 같을 수가 없다. 위에서 put_queens 함수를 보면 행을 기준으로 나누고 있기 때문이다.
만약 열의 값이 같거나(col[i] == col) 윗쪽 대각선에서 만나거나 (col[i] - i == col - rows) 아랫쪽 대각선에서 만나면(col[i] + i == col + rows) 문제를 해결하지 못한 것이기 때문에 False 값을 반환한다.
그런 문제 없이 끝까지 검사가 끝났다면 True 값을 반환한다.
def show_board(self):
for row in range(self.size):
line = ""
for column in range(self.size):
if self.col[row] == column:
line += "Q "
else:
line += "+ "
print(line)
print("\n")show_board() 함수이다.
행을 size 만큼 반복문을 돌리고, 열을 size만큼 반복문을 돌려서 행*열( = size * size)만큼의 체스 보드를 출력한다.
매 행의 line은 ""로 비어있다.
각 행의 열을 반복문을 통해 돌려 col이라는 queen을 놓은 자리를 저장한 리스트의 열의 값과 반복문의 열의 값이 같다면 Q를, 아니면 +를 출력한다.
N = 6
q = NQueens(N)
q.solve()예제에서는 6-Queens 문제를 해결했다.

댓글 열어뒀습니다.
질문이나 수정 사항 있다면 알려주세요.



