| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Reflected
- pwnable
- bWAPP
- beebox
- htmlinjection
- 유석종교수님
- basicrce3
- SISS
- Systemhacking
- c
- mount
- grafana
- 백준
- cloud
- CodeEngn
- datastructure
- backjoon
- python
- 와이어샤크
- 자료구조
- System
- wireshark
- EC2
- AWS
- Dreamhack
- acc
- Reversing
- Linux
- fork-bomb
- cgroup
- Today
- Total
Ctrl + Shift + ESC
CHAPTER 01 자료구조 개요 본문
1.1 소프트웨어와 자료구조
소프트웨어 : 특정 기능을 담당하는 단일 또는 복수의 프로그램
프로그램은 처리할 대상인 자료(데이터)와 처리 절차인 알고리즘으로 구성되며, 프로그램을 설계하는 작업을 프로그래밍 또는 코딩이라고 부른다.
자료구조 : 프로그램을 통해 대량의 데이터를 효과적으로 저장하고 처리하기 위한 방법론 또는 자료구조 그 자체
형태에 따라 선형 자료구조(배열, 스택, 큐, 리스트)와 비선형 자료구조(트리, 그래프), 구현 방법에 따라 배열 방식과 연결 리스트 방식으로 구분
그 외 정렬, 탐색, 해싱 등의 관련 알고리즘도 자료구조의 학습 범위에 포함된다.
1.2 소프트웨어 개발 주기
소프트웨어는 요구사항, 문제 분석, 기능 설계, 구현, 검증의 5단계에 걸쳐 개발되고 단계를 순환하면서 개선된다.
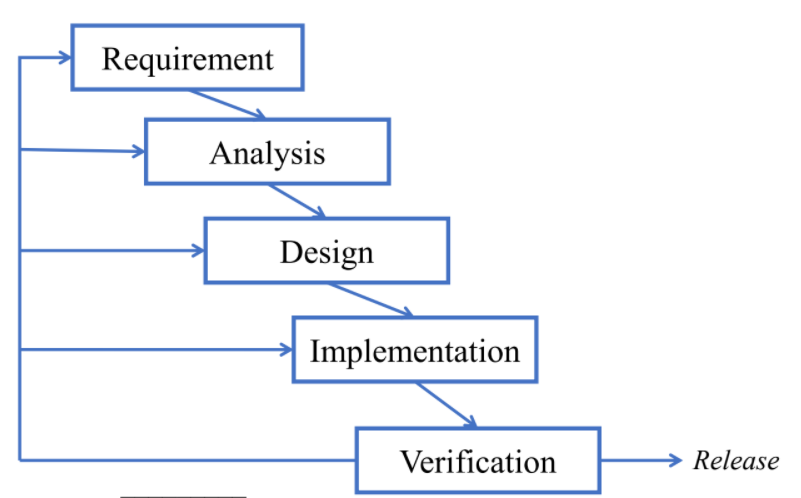
요구사항(requirement) 단계에서는 개발하려는 소프트웨어의 목표를 정의한다.
이 단계에서는 소프트웨어의 목표 사용 환경(platform), 기능(function), 입출력, 사용자 인터페이스 등의 정보를 요구사항 명세서에 기록한다.
문제 분석(analysis) 단계에서는 추상적으로 기술된 소프트웨어의 요구 사항을 해결하기 용이하도록 구체적인 세부 문제들로 분할한다.
대표적인 문제 분석 기법에는 하향식과 상향식 방법이 있다.
하향식(top-down)은 프로젝트의 최상위 목표에서 하위 단계로 세부 모듈들을 분리해가는 방식으로 전체 모듈의 계층도를 생성한다.
상향식(bottom-up)은 기본 모듈들을 조합하여 서브 시스템을 완성하고 이 서브 시스템을 다시 결합하여 최종적인 목표 시스템을 구축한다.
설계(design) 단계는 전 단계에서 생성된 모듈에서 필요한 객체와 연산들을 정의한다.
객체는 속성과 메소드로 이루어진다.
구현(implementation)은 각 모듈에서 사용하는 객체와 메소드 함수를 실행가능한 코드로 만드는 코딩 과정을 말한다.
메소드는 기본 내장 함수를 이용하거나 직접 알고리즘을 설계하여 개발할 수 있다.
검증(verification)은 구현된 프로그램이 프로젝트의 목표 기능들을 정확히 수행하고 오류가 없는지 확인하는 과정이다.
일반적으로 데이터셋을 이용한 시험 방법을 사용한다.
시험은 입력 데이터와 출력 결과만으로 판단하는 블랙 박스 시험과 입력과 출력 정보 이외에 프로그램 내부 루틴까지 포함하여 오류를 검사하는 화이트 박스 시험으로 나뉜다.
평가 결과에서 오류가 발생하면 오류의 원인에 해당하는 전 단계로 돌아가서 개선 절차를 수행해 목표 수준에 도달할 때까지 이 단계들을 반복하면서 순환한다.
1.3 알고리즘의 정의
알고리즘(algorithm)은 주어진 문제 해결에 필요한 유한한 명령어들의 집합으로 정의하며, 다음의 조건을 만족해야 한다.
1. 입력(input) : 0개 이상의 입력이 있어야 한다.
2. 출력(output) : 1개 이상의 출력이 있어야 한다.
3. 명확성(definiteness) : 모호하지 않은 명령어로 표현되어야 한다.
4. 유한성(finiteness) : 유한한 수의 명령어로 이루어져야 한다.
5. 유효성(effectiveness) : 중복되고 불필요한 명령문 없이 효율적으로 작성되어야 한다.
비교적 단순한 알고리즘은 플로우 차트로 표현할 수 있고, 일반적으로는 알고리즘을 빠르게 기술하기 위해 의사 코드(pseudo code)를 사용한다.
프로그램 1.1) 피보나치 수열
피보나치 수열은 특정 원소의 값을 이전 두 개 원소의 합으로 계산한다.
피보나치 수열 프로그램은 100,000보다 작은 피보나치 수들을 계산하여 출력해준다.
fibo() 함수에서 변수 a와 b가 특정 원소 앞의 두 원소일 때, 이 값들로 새로운 원소 값을 계산하고 변수 a와 b를 업데이트하여 재사용하도록 한다.
def fibo(fb) :
a = 0
b = 1
while True :
a,b = b, a+b
if b > n : break
fb.append(b)
n = 100000
fb = [0, 1]
fibo(fb)
print(fb)
print("# of fibos", len(fb))코드를 살펴보았다.
n = 100000
fb = [0, 1]
fibo(fb)
def fibo(fb) :
a = 0
b = 1
while True :
a,b = b, a+b
if b > n : break
fb.append(b)fibo 함수이다.
첫번째 항 0과 두번째 항 1은 고정이기 때문에 값에 넣어준다.
a값을 b로, b값을 a+b로 바꿔준다.
b가 n(100000)보다 작은 동안 반복문이 계속 반복되고, b의 값을 리스트 fb에 추가한다.
print(fb)
print("# of fibos", len(fb))fb 리스트를 출력한 뒤에 len(fb)를 통해 원소의 개수를 출력한다.

프로그램 1.2) 소수 찾기
1과 자기 자신으로만 나누어지는 소수(prime number)를 탐색하는 프로그램을 작성해 보자.
소수 찾기 프로그램은 1000보다 작은 모든 소수를 탐색하여 출력하는 예제이다.
실행 결과와 같이 소수의 분포를 시각화하기 위하여 소수가 아닌 값은 점('.')으로 표시하였다.
뒤로 갈수록 소수의 빈도가 점차 낮아지는 것을 알 수 있다.
def find_prime(num) :
for i in range(2, num+1) :
prime = 1
for j in range(2, i):
if i % j == 0 :
prime = 0
break
if prime:
prime_list.append(i)
max_num = 1000
prime_list = []
find_prime(max_num)
for i in range(2, max_num):
if i in prime_list:
print('%3d' % i, end = '')
else:
print('.', end = '')
if i % 50 == 0:
print()
print()
print('# of prime numbers = ', len(prime_list))코드를 살펴보았다.
max_num = 1000
prime_list = []
find_prime(max_num)소수의 최대값 max_num을 1000으로 지정하고 소수를 담을 prime_list를 만들었다.
함수 find_prime을 통해 소수를 찾는다.
def find_prime(num) :
for i in range(2, num+1) :
prime = 1
for j in range(2, i):
if i % j == 0 :
prime = 0
break
if prime:
prime_list.append(i)반복문 i를 통해 2에서 num까지 반복한다.
여기서 prime의 값이 1인 이유는 True로 설정하기 위해서이다.
반복문 j를 통해 2부터 i-1까지 반복한다.(1은 소수에 포함되지 않고, i가 포함되면 자기 자신과 나누어 떨어지므로 포함되면 안된다.)
i가 j, 즉 자신보다 작은 수로 나누어떨어진다면 소수가 아니기 때문에 prime 값을 0(False)로 바꾼다.
반복문 j가 끝나면 if문을 통해 소수인지를 판단하고, 소수라면 prime_list에 추가한다.
for i in range(2, max_num):
if i in prime_list:
print('%3d' % i, end = '')
else:
print('.', end = '')
if i % 50 == 0:
print()반복문을 통해 소수라면 값을, 소수가 아니라면 .을 출력한다.
50번째 숫자를 기준으로 줄을 바꾼다.
print()
print('# of prime numbers = ', len(prime_list))줄을 바꾼 뒤에 len(prime_list)를 통해 소수의 개수를 출력한다.

1.4 추상 자료형
추상 자료형(abstract data type:ADT) : 프로그래밍 언어에서 실 세계 객체를 기본 자료형으로 지원한 것
이에 기반한 작업을 객체 지향 프로그래밍(object oriented programming)이라고 한다.
파이썬, C++, 자바는 기본적으로 추상 자료형인 클래스를 지원하지만 C언어는 지원하지 않는다.
프로그램 1.3) 분수 연산과 출력
프로그램에서 실수를 출력하는 것은 쉽지만 분수의 출력은 기본적으로 지원하지 않는다.
분수 자료형을 클래스 Fraction으로 선언하여 분수 연산과 출력 함수를 작성해 보자.
분수는 약분하여 출력해야 하므로 분자와 분모를 최대 공약수(gcd)로 나눈 후에 출력한다.
최대 공약수를 구하는 공식은 다음과 같다.
gcd(x,y) = gcd(y, x%y) if y>0
gcd(x, 0) = xy가 0이 되는 시점의 x값이 최대 공약수가 된다.
class Fraction:
def __init__(self, up, down):
self.num = up
self.den = down
def __str__(self):
return str(self.num)+"/"+str(self.den)
def gcd(self, a, b):
while a % b != 0:
a, b = b, a % b
return b
def __add__(self, other):
new_num = self.num*other.den + self.den*other.num
new_den = self.den*other.den
common = self.gcd(new_num, new_den)
return Fraction(new_num//common, new_den//common)
def multiply(self, other):
new_num = self.num*other.num
new_den = self.den*other.den
common = self.gcd(new_num, new_den)
return Fraction(new_num//common, new_den//common)
num1 = Fraction(1, 4) # 1/4
num2 = Fraction(1, 2) # 1/2
num3 = num1 + num2
print(num1, "+", num2, "=", num3)
num1 = Fraction(2, 3)
num2 = Fraction(4, 5)
num3 = num1 + num2
print(num1, "+", num2, "=", num3)
num1 = Fraction(2, 5)
num2 = Fraction(3, 8)
num3 = num1.multiply(num2)
print(num1, "*", num2, "=", num3)
num1 = Fraction(3, 4)
num2 = Fraction(2, 9)
num3 = num1.multiply(num2)
print(num1, "*", num2, "=", num3)코드를 살펴보았다.
class Fraction:
def __init__(self, up, down):
self.num = up
self.den = downclass Fraction에 __init__ 이라는 메서드를 정의했는데, 이를 연산자 중복이라고 부른다.
연산자 중복(overload)란 특별한 메서드를 사용해서 연산자가 하는 일을 정의하는 것이다.
연산자 중복을 이용하면 사용자가 직접 만든 클래스의 객체에 대해서도 자료형처럼 연산자를 사용할 수 있다.
특히 __init__이라는 메서드는 초기화 메서드라고 불린다.
여기에서는 초기화 메서드를 통해서 num에 up, den에 down 값을 입력했다.
def __str__(self):
return str(self.num)+"/"+str(self.den)__str__ 메서드를 통해 str로 형변환을 했다.
해당 메서드를 통해서 분수 형태로 출력할 수 있게 되었다.
def gcd(self, a, b):
while a % b != 0:
a, b = b, a % b
return b최소공약수를 구하는 함수 gcd이다.
a가 b로 나누어 떨어지지 않는 동안 a의 값을 b로, b의 값을 a를 b로 나눈 나머지로 바꾼다.
a가 b로 나누어 떨어지면, 즉 b가 처음의 a와 b의 최대공약수가 되면 b를 return한다.
def __add__(self, other):
new_num = self.num*other.den + self.den*other.num
new_den = self.den*other.den
common = self.gcd(new_num, new_den)
return Fraction(new_num//common, new_den//common)__add__를 통해 분수의 뎃셈을 한다.
덧셈은 두 분수를 통분한 뒤에 해야 하므로 각각의 분모와 분자를 크로스해서 곱한 뒤 더한다.
common에 new_num과 new_den의 최대공약수를 구한 뒤 약분된 형태로 return한다.
def multiply(self, other):
new_num = self.num*other.num
new_den = self.den*other.den
common = self.gcd(new_num, new_den)
return Fraction(new_num//common, new_den//common)multiply는 연산자 중복 형태가 아니므로 함수의 형태를 맞춰 입력해야 실행할 수 있다.
각 분수의 분자와 분모를 곱한 뒤 약분하기 위해 add처럼 최대공약수를 구해 약분된 형태로 return한다.
num1 = Fraction(1, 4) # 1/4
num2 = Fraction(1, 2) # 1/2
num3 = num1 + num2
print(num1, "+", num2, "=", num3)덧셈 예시를 한 가지 살펴보았다.
num1의 분자에 1, 분모에 4를 입력했다.
num2의 분자에 1, 분모에 2를 입력했다.
__add__ 메서드는 연산자 중복을 이용했기 때문에 +를 통해 실행할 수 있다.
두 분수를 더한 뒤 print 함수를 통해 값을 출력한다.
num1 = Fraction(2, 5)
num2 = Fraction(3, 8)
num3 = num1.multiply(num2)
print(num1, "*", num2, "=", num3)곱셈 예시를 한 가지 살펴보았다.
num1의 분자에 2, 분모에 5를 입력했다.
num2의 분자에 3, 분모에 8을 입력했다.
multiply 메서드는 연산자 중복을 이용하지 않았기 때문에 함수의 형태를 지켜 입력해야 실행할 수 있다.
두 분수를 곱한 뒤 print 함수를 통해 값을 출력한다.

1.5 프로그램 성능 평가
성능 평가(performance evaluation) : 개발된 프로그램을 평가하는 작업
정량적 성능 평가 기준(구체적인 기준 O)으로 공간 복잡도(space complexity)와 시간 복잡도(time complexity)를 사용한다.
공간 복잡도
공간 복잡도 : 프로그램의 수행을 완료하는데 필요한 메모리의 양(memory space)
알고리즘이 사용하는 메모리 공간은 다시 고정 요구 공간과 가변 요구 공간으로 구분한다.
고정 요구 공간(fixed memory space) : 프로그램이 실행 중에 크기의 변동이 없는 메모리 공간
ex) 프로그램 명령어, 고정 크기 변수, 상수 등
가변 요구 공간(variable memory space) : 프로그램 실행 중에 요청되어 크기를 예측하기 어려운 경우 - 공간 복잡도 평가에서 중요!
ex) 배열 전달, 재귀 호출 등의 요소가 포함되는 경우
def calc(a, b, c, d):
return (a * c + a * d ) - (b * c + b * d)위의 calc() 함수는 컴파일 이후 변경되지 않는 고정 공간 변수만 사용하고 있으므로 가변 요구 공간은 0이다.
def factorial(n):
if n > 0:
return n * factorial(n - 1)
return 1위의 factorial() 함수는 재귀 호출을 통해 팩토리얼 계산을 수행한다.
함수는 호출 시마다 매개변수, 지역변수, 회귀 주소(return address)를 저장해야 하기 때문에 재귀 호출 횟수에 비례해서 가변 공간이 증가한다.
위 함수의 공간 복잡도 = n * (size(num) + return address)이다.
시간 복잡도 : 프로그램의 수행을 완료하는데 걸리는 시간(computation time)
컴파일 시간(compile time), 실행 시간(execution time)로 구분하는데, 실행 시간이 가변적이기 때문에 시간 복잡도 평가에서 더 중요하다.
시간 복잡도 계산을 위해 실행 시간을 측정하는 방법은 환경에 따라 달라지므로 실행 시간보다는 실행하는 명령문의 수를 시간 복잡도로 사용한다.
명령문 측정표의 작성 방법은 다음과 같다.
1. 한 문장에 포함된 명령문의 수(steps/execution)를 결정한다.
2. 이 문장의 실행 횟수를 (명령문 * 반복 횟수)로 계산한다.
3. 전체 문장의 실행 횟수를 모두 합산한다.
|
|
명령문 수
|
빈도 수
|
총 횟수
|
|
def factorial(n) :
|
0
|
0
|
0
|
|
if n :
|
1
|
n+1
|
n+1
|
|
return n * factorial(n-1)
|
1
|
n
|
n
|
|
return 1
|
1
|
1
|
1
|
|
|
|
|
2n+2
|
if n 문장은 프로그램 실행 중에 True인 경우가 n번, False인 경우가 1번이므로 총 n+1번 실행된다.
그 다음 return 문은 if 조건식이 True인 경우에만 n번 수행된다.
마지막 return 문은 총 1회만 실행된다.
따라서 이 factorial() 함수에서 실행되는 명령문의 총 수는 2n+2가 된다.
|
|
명령문 수
|
빈도 수
|
총 횟수
|
|
def matrix() :
|
0
|
0
|
0
|
|
for i in range(n) :
|
1
|
n
|
n
|
|
for j in range(n) :
|
1
|
n * n
|
n * n
|
|
c[i][j] = a[i][j] + b[i][j]
|
1
|
n * n
|
n * n
|
|
|
|
|
2n^2 + n
|
반복문 i는 0에서부터 n-1까지 n번 반복된다.
반복문 j는 반복문 i가 n번 반복될 동안 0에서부터 n-1까지 n번 반복되므로 n * n번 실행된다.
c[i][j]는 반복문 j가 실행될 때 함께 실행되므로 역시 n * n번 실행된다.
따라서 이 matrix() 함수에서 실행되는 명령문의 총 수는 2n^2 + n가 된다.
점근적 표기법
점근적 표기법(asymptotic notation) : 입력의 수(n)가 증가할 때 알고리즘의 시간 복잡도의 변화 패턴을 표현하는 방법
알고리즘 성능에 영향을 크게 미치는 고차항 부분만을 취하여 근사적으로 표기한다.
점근적 표기법은 시간 복잡도의 상한선(upper bound) 또는 하한선(lower bound)의 유무에 따라 기호를 사용하여 표현한다.
빅 오 시간 복잡도


빅 오메가 시간 복잡도


빅 세타 시간 복잡도


시간 복잡도 함수의 종류
상수형 시간 복잡도는 n에 무관하게 항상 일정한 수(k)의 명령어 수행한다는 의미이다.
지수형이나 팩토리얼형 함수는 n이 조금만 커져도 처리할 명령문의 수가 급속히 증가하므로 n이 작은 경우에 사용해야 한다.

질문이나 수정 사항 있다면 알려주세요.


