| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Linux
- 와이어샤크
- beebox
- Reflected
- AWS
- 자료구조
- mount
- cloud
- 유석종교수님
- pwnable
- c
- python
- backjoon
- Dreamhack
- datastructure
- Reversing
- EC2
- htmlinjection
- docker
- SISS
- fork-bomb
- bWAPP
- basicrce3
- acc
- CodeEngn
- 백준
- Systemhacking
- wireshark
- cgroup
- System
- Today
- Total
Ctrl + Shift + ESC
[Dreamhack] Cryptography STAGE 2 - 고전 암호와 현대 암호 : 고전 암호 본문
서론

고전 암호는 컴퓨터와 같은 고성능 연산 장치가 발명되기 전에, 비교적 간단한 기계와 손 등으로 암복호화를 수행하던 암호를 말한다.
대부분 컴퓨터를 사용하면 쉽게 복호화되기 때문에 현대에는 사용되지 않는다.
고전 암호는 일반적으로 치환(Substitution)과 전치(Transposition)의 방법으로 설계된다.
치환은 평문의 문자를 다른 문자로 바꾸는 것을 말하며, 전치는 평문 문자들의 위치를 바꾸는 것을 말한다.
단순한 고전 암호는 한 가지 원리만을 사용하는 치환 암호(Substitution Cipher) 또는 전치 암호(Transposition Cipher)이고, 복잡한 고전 암호는 두 원리를 모두 사용한다.
치환 암호는 단일 문자 치환 암호(Monoalphabetic Substitution Cipher)와 다중 문자 치환 암호(Polyalphabetic Substitution Cipher)로 나누어진다.
단일 문자 치환 암호
단일 문자 치환 암호(Monoalphabetic Substitution Cipher) : 평문의 각 문자를 약속된 다른 문자로 치환하는 암호
복호화를 위해 치환의 대응 관계는 일대일 대응이다.
평문의 'A'가 암호문의 'B'로 치환된다면, 평문의 다른 어떤 문자도 'B'로 치환되지 않는다.
카이사르 암호
단일 문자 치환 암호의 대표적인 예로 기원전 44년 줄리어스 카이사르가 사용한 카이사르 암호(Caesar Cipher)가 있다.
카이사르 암호는 평문의 각 알파벳을 일정한 거리만큼 밀어서 다른 알파벳으로 치환한다.
이를 복호화할 때는 암호문의 각 문자를 다시 원래 위치로 밀어서 평문을 구한다.
송신자와 수신자가 몇 칸을 밀 것인지를 사전에 합의해야 통신이 이뤄질 수 있다.
카이사르 암호는 알파벳을 밀어낸 횟수만 알면 해독할 수 있다.
알파벳을 밀어낸 횟수를 키(Key)라고 한다면, 알파벳은 총 26자이므로 가능한 키의 갯수는 26개이다.
암호학에서 가능한 모든 키의 집합을 키 공간(Key Space)이라고 하는데, 이를 이용하여 다시 표현하면 카이사르 암호에서 키 공간의 크기는 26이다.

알파벳 A부터 Z를 0부터 25까지 대응 시키면, n글자씩 밀어내는 카이사르 암호를 위의합동식으로 표현할 수 있다.
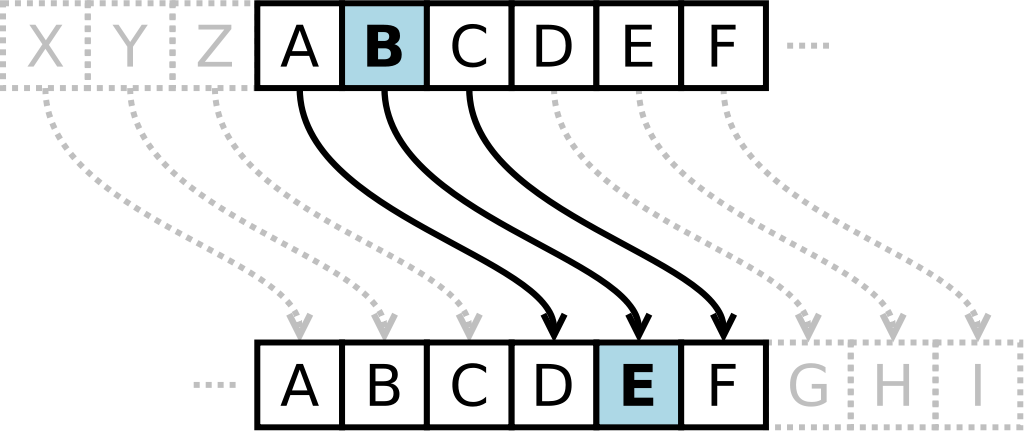
위는 오른쪽으로 3번 밀어내는 카이사르 암호를 도식화한 것이다.
이를 이용하여 'BEEF'를 암호화하면 'EHHI'가 출력된다.
아래는 카이사르 암호화 소스코드이다.
def encipher(p, k):
c = ''
for i in range(len(p)):
a = ord(p[i])
if a == 32: a = 64
t = a + k
if t > 90: t -= 27
if t == 64: t = 32
c += chr(t)
return c암호화 코드는 평문 p와, key k를 매개변수로 받는다
구해야 할 암호문을 C로 정의한 다음 평문의 길이만큼 반복문을 돌려준다.
아스키 코드 33~64는 사용하지 않기 때문에 뛰어쓰기(32) 다음 A값(65)으로 넘어간다.
또한 Z값(90) 다음 다시 앞으로 돌아가기 때문에 만약 아스키값이 90보다 크다면 - 27을 해줘 다시 앞 문자로 돌아갈 수 있도록 맞춘다.
위의 원리를 이용하면 카이사르 복호화 소스코드도 작성할 수 있다.
def decipher(p, k):
c = ''
for i in range(len(p)):
a = ord(p[i])
if a == 32: a = 91
t = a - k
if t < 65: t += 27
if t == 91: t = 32
c += chr(t)
return c
춤추는 인형과 코드북 암호
카이사르 암호는 알파벳을 밀어서 암호화하는 특성상, 키 공간의 크기가 26으로 작기 때문에 컴퓨터를 사용하여 반복문을 통해 26개의 경우를 살펴보면 쉽게 복호화된다.
조금 더 복잡한 단일 치환암호로는 셜록 홈즈에 나온 춤추는 인형 암호가 있다.
이 암호는 사람 한 명이 글자 하나에 대응된다.
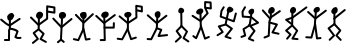
춤추는 인형 암호처럼 모든 알파벳을 서로 다른 기호와 무작위로 일대일 대응시켜 치환하면 키 공간의 크기는 26!이 된다.
이 정도 크기의 키 공간은 현대의 컴퓨터로도 전부 탐색하기 어렵다.
그러나 단일 치환 암호는 언어가 지닌 통계적 특성이 유지된다는 단점이 있다.
통계적으로, 영어 문장에서 가장 많이 사용되는 알파벳은 e이다.
따라서 단일 치환 암호가 적용된 어떤 암호문에서 b가 가장 많이 등장한다면, b는 e가 치환된 것이라 추측할 수 있다.
이 특성을 이용하면 일반적인 영문 단일 치환 암호문은 어렵지 않게 해독될 수 있다.
실제로 작중에서 셜록 홈즈도 해당 방법을 통해 암호를 해독했다.
난수표나 코드북을 이용한 단일 치환 암호는 현재도 종종 사용된다.
송신자와 수신자가 책을 정하고, 송신자가 책의 페이지 \(x\)와 단어의 인덱스 \(y\)를 보내면, 수신자는 책 \(x\)페이지의 \(y\)번째 단어를 확인하여 송신자의 메세지를 해독한다.
이 암호 체계는 공작원에게 지령을 전달하는 목적으로 최근에도 쓰이고 있다.

예를 들어 아래와 같은 책을 공유하고, 송신자가 21537, 21529, 21406, 21402라는 암호문을 보내면 수신자는 215 페이지의 37번째 단어, 215 페이지의 29번째 단어, 214 페이지의 6번째 단어, 214 페이지의 2번째 단어를 찾고, 이를 이어 붙여 come to yellow roads 라는 메세지를 구할 수 있다.
다중 문자 치환 암호
다중 문자 치환 암호(Polyalphabetic Substitution Cipher) : 평문의 한 문자가 암호문에서 여러 종류의 문자로 치환될 수 있는 암호
대표적인 다중 문자 치환 암호로는 비제네르 암호(Vigenere Cipher)가 있다.
비제네르 암호에서 암호화와 복호화는 미리 정해진 키워드를 통해 이루어진다.
'SKY'라는 키워드로 평문 'DREAMHACK'을 비제네르 암호화하는 과정은 다음과 같다.

우선 위와 같은 비제네르 표에서, 키의 각 문자인 'S', 'K', 'Y'행을 고른다.
그 뒤, 키워드를 반복하며 키워드의 각 행에서 평문의 문자에 대응되는 문자로 평문을 치환한다.
| 키 | S | K | Y | S | K | Y | S | K | Y |
| 평문 | D | R | E | A | M | H | A | C | K |
| 암호문 | V | B | C | S | W | F | S | M | I |
A부터 Z를 0부터 25까지 대응시키면 비제네르 암호를 다음의 합동식으로 표현할 수 있다.
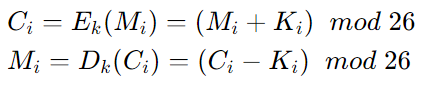
여기서 는 암호문, 은 평문, 는 키워드를 의미하고, 는 의 i번째 요소를 나타낸다.
아래는 비제네르 암호를 풀어주는 사이트이다.
https://www.mygeocachingprofile.com/codebreaker.vigenerecipher.aspx
My Geocaching Profile.com - Vigenere Cipher Codebreaker
www.mygeocachingprofile.com
전치 암호
전치 암호(Transposition Cipher) : 평문을 구성하는 문자들의 순서를 재배열한 암호문
평문을 정해진 길이의 블록들로 나누고, 규칙을 적용하여 블록 안의 문자들을 재배치한다.

예를 들어, 블록의 길이가 3이고 키가 (3,1,2)일 때 평문 DREAM HACK의 암호화는 위과 같이 이루어진다.

전치 암호의 대표적인 예시로는 기원전 450년에 고대 그리스인들이 발견한 스키테일 암호(Scytale Cipher)가 있다.
이 암호는 나무봉(Scytale)을 이용한 암호로, 먼저 메세지를 교환할 두 사람이 같은 크기의 나무봉을 제작한다.
그 뒤, 송신자는 종이 테이프를 나무봉에 감고, 테이프 위에 세로로 메세지를 기입하여 암호문를 만든다.
종이테이프를 풀어내면 순서가 뒤섞여 메세지를 읽을 수 없지만, 같은 나무봉을 가진 수신자는 테이프를 다시 나무봉에 감아서 이를 해석할 수 있다.
고전 암호 공격
안전하다고 여겨졌던 고전 암호들은 암호 분석 도구와 기술의 발달로 쉽게 분석되었다.
고전 암호를 공격하는 방법으로는 대표적으로 전수 키 탐색 공격(Exhaustive Key Search Attack)과 빈도수 분석(Frequency Analysis)이 있다.
전수 키 탐색 공격
전수 키 탐색 공격(Exhaustive Key Search Attack) : 평문과 암호문을 알 때, 키 공간을 전부 탐색하며 주어진 암호문과 같은 암호문을 생성하는 키를 찾는 방법
굉장히 단순한 공격 방법이지만 키 공간의 크기가 작다면 빠른 시간안에 키를 찾고, 암호를 해독할 수 있다.
단일 치환 암호인 카이사르 암호는 키 공간이 26으로 매우 작기 때문에 전수 키 탐색 공격에 취약하다.
빈도수 공격
단일 치환 암호는 평문의 문자와 암호문의 문자가 항상 일대일 대응을 이루기 때문에 평문의 통계적 특성이 유지된다.
예를 들어, 영어 문장에서 각 알파벳이 사용되는 빈도를 그래프로 표현하면 아래과 같은데, 이런 특성은 문자를 단일 치환해도 유지된다.

위에 따르면 평문의 E를 A로 치환해서 암호문을 만들었다면, 암호문에서 가장 많이 등장하는 알파벳이 A일 가능성이 높다.
이런 추측을 바탕으로 암호문을 복구하는 것을 빈도수 분석(frequency analysis)이라고 한다.
이는 암호문이 어떤 언어로 구성되어 있어도 대상 언어의 특성을 안다면 시도해볼 수 있다.
다중 치환 암호는 이러한 통계적 특성이 사라지기 때문에, 빈도수 공격으로부터 비교적 안전하다고 알려져 있다.


